Section 6.5 : More Volume Problems
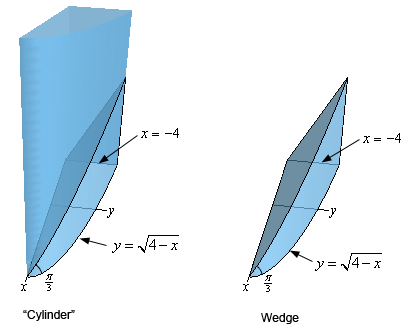
4. Find the volume of a wedge cut out of a “cylinder” whose base is the region bounded by \(y = \sqrt {4 - x} \), \(x = - 4\) and the \(x\)-axis. The angle between the top and bottom of the wedge is \(\frac{\pi }{3}\). See the figure below for a sketch of the “cylinder” and the wedge (the positive \(x\)-axis and positive \(y\)-axis are shown in the sketch – they are just in a different orientation).
Show All Steps Hide All Steps
Start SolutionWhile not strictly needed let’s redo the sketch of the “cylinder” and wedge from the problem statement only this time let’s also sketch in what the cross-section will look like.
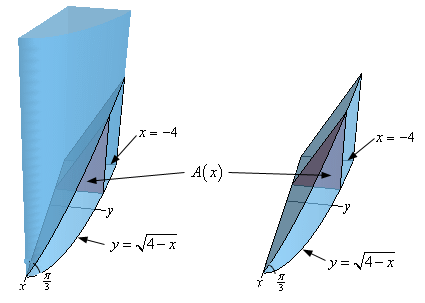
Because the cross-section is perpendicular to the \(x\)-axis as we move the cross-section along the \(x\)-axis we’ll change its area and so the cross-sectional area will be a function of \(x\), i.e. \(A\left( x \right)\). Also note that as shown in the sketches the cross-section will be a right triangle.
While the sketches above are nice to get a feel for what the solid and cross-sections look like, what we really need is just a sketch of just the cross-section. So, here are a couple of sketches of the cross-sectional area.
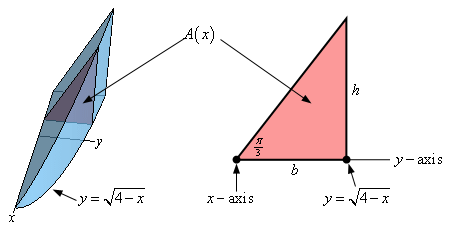
The sketch on the left is just pretty much the sketch we’ve seen before and is included to give us a reference point for the actual cross-section that is shown on the right.
As noted in the sketch on the right we’ll call the base of the triangle \(b\) and the height of the triangle \(h\). Also, the dot on the left side of the base represents where the \(x\)-axis is on the cross-section and the dot on the right side of the base represents the curve that defines the edge of the solid (and hence the wedge).
From this sketch it should then be pretty clear that the length of the base is simply the distance from the \(x\)-axis to the curve or,
\[b = \sqrt {4 - x} \]Likewise, the height can be found from basic right triangle trig.
\[\tan \left( {\frac{\pi }{3}} \right) = \frac{h}{b}\hspace{0.5in} \Rightarrow \hspace{0.5in}h = b\tan \left( {\frac{\pi }{3}} \right) = \sqrt 3 \sqrt {4 - x} \]So, a formula for the area of the cross-section in terms of \(x\) is then,
\[A\left( y \right) = \frac{1}{2}bh = \frac{{\sqrt 3 }}{2}{\left( {\sqrt {4 - x} } \right)^2} = \frac{{\sqrt 3 }}{2}\left( {4 - x} \right)\]Finally, we need the volume itself. We know that the volume is found by evaluating the following integral.
\[V = \int_{a}^{b}{{A\left( x \right)\,dx}}\]From the sketches in the problem statement or from Step 1 we can see that the “first” cross-section will occur at \(x = - 4\) (the back end of the “cylinder”) and the “last” cross‑section will occur at \(x = 4\) (the front end of the “cylinder” where the curve intersects with the \(x\)-axis. These are then the limits for the integral.
The volume is then,
\[V = \int_{{ - 4}}^{4}{{\frac{{\sqrt 3 }}{2}\left( {4 - x} \right)\,dx}} = \left. {\frac{{\sqrt 3 }}{2}\left( {4x - \frac{1}{2}{x^2}} \right)} \right|_{ - 4}^4 = \require{bbox} \bbox[2pt,border:1px solid black]{{16\sqrt 3 }}\]