Section 4.5 : The Shape of a Graph, Part I
12. For \(g\left( x \right) = x - 2\ln \left( {1 + {x^2}} \right)\) answer each of the following questions.
- Identify the critical points of the function.
- Determine the intervals on which the function increases and decreases.
- Classify the critical points as relative maximums, relative minimums or neither.
Show All Solutions Hide All Solutions
a Identify the critical points of the function. Show SolutionWe need the 1st derivative to get the critical points so here it is.
\[g'\left( x \right) = 1 - 2\frac{{2x}}{{1 + {x^2}}} = \frac{{1 - 4x + {x^2}}}{{1 + {x^2}}}\]Now, recall that critical points are where the derivative doesn’t exist or is zero. Because we simplified and factored the derivative as much as possible we can clearly see that the derivative will exist everywhere (or at least the denominator will not be zero for any real numbers…). We’ll also need the quadratic formula to determine where the numerator, and hence the derivative, is zero. The critical points of this function are then,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{x = 2 \pm \sqrt 3 = 0.2679,\,\,\,3.7321}}\]b Determine the intervals on which the function increases and decreases. Show Solution
To determine the increase/decrease information for the function all we need is a quick number line for the derivative. Here is the number line.
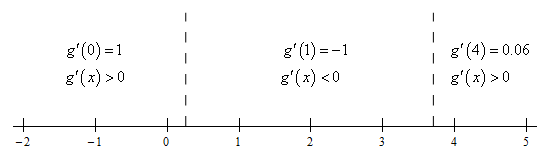
From this we get the following increasing/decreasing information for the function.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{Increasing : }}\left( { - \infty ,0.2679} \right)\,\,\,\,\,\& \,\,\,\,\,\left( {3.7321,\infty } \right)\hspace{0.25in}\hspace{0.25in}{\mbox{Decreasing : }}\,\,\left( {0.2679,3.7321} \right)}}\]c Classify the critical points as relative maximums, relative minimums or neither. Show Solution
With the increasing/decreasing information from the previous step we can easily classify the critical points using the 1st derivative test. Here is classification of the functions critical points.
\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{align*}x & = 0.2679\,\,\,\,\,\,:\,{\mbox{ Relative Maximum}}\\ x & = 3.7321\,\,\,\,\,\,\,:\,{\mbox{ Relative Minimum}}\end{align*}}\]