Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 4.6 : The Shape of a Graph, Part II
1. The graph of a function is given below. Determine the intervals on which the function is concave up and concave down.
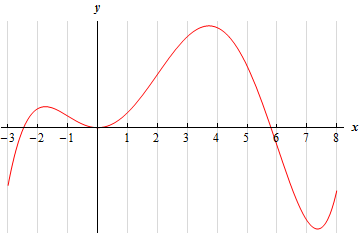
There really isn’t too much to this problem. We can easily see from the graph where the function in concave up/concave down and so all we need to do is estimate where the concavity changes (and this really will be an estimate as it won’t always be clear) and write down the intervals.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{Concave Up : }}\left( { - 1,2} \right)\,\,\,\& \,\,\,\left( {6,\infty } \right)\hspace{0.5in}{\mbox{Concave Down : }}\,\,\left( { - \infty , - 1} \right)\,\,\,\,\& \,\,\,\,\left( {2,6} \right)}}\]Again, the endpoints of these intervals are, at best, estimates as it won’t always be clear just where the concavity changes.