Section 4.6 : The Shape of a Graph, Part II
12. For \(Q\left( t \right) = 3t - 8\sin \left( {{ \displaystyle \frac{t}{2}}} \right)\) on \(\left[ { - 7,4} \right]\) answer each of the following questions.
- Identify the critical points of the function.
- Determine the intervals on which the function increases and decreases.
- Classify the critical points as relative maximums, relative minimums or neither.
- Determine the intervals on which the function is concave up and concave down.
- Determine the inflection points of the function.
- Use the information from steps (a) – (e) to sketch the graph of the function.
Show All Solutions Hide All Solutions
a Identify the critical points of the function. Show SolutionThe parts to this problem (with the exception of the last part) are just like the basic increasing/decreasing problems from the previous section and the basic concavity problems from earlier in this section. Because of that we will not be putting in quite as much detail here. If you are still unsure how to work the parts of this problem you should go back and work a few of the basic problems from the previous section and/or earlier in this section before proceeding.
We will need the 1st derivative to start things off.
\[\underline {Q'\left( t \right) = 3 - 4\cos \left( {{\frac{t}{2}}} \right)} \]From the 1st derivative all of the critical points are,
\[\begin{array}{*{20}{c}}{t = 1.4454 + 4\pi n}\\{t = 11.1210 + 4\pi n}\end{array}\hspace{0.5in}n = 0,\, \pm 1,\, \pm 2,\, \pm 3, \ldots \]If you need some review of the solving trig equation process go back to the Solving Trig Equations sections for some examples.
Plugging in some values of \(n\) we see that the critical points in the interval \(\left[ { - 7,4} \right]\) are,
\[\underline {t = - 1.4454\,\,\,\,\,\,\,\,\& \,\,\,\,\,\,\,t = 1.4454} \]b Determine the intervals on which the function increases and decreases. Show Solution
To answer this part all we need is the number line for the 1st derivative.
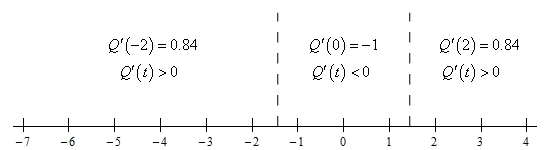
From this we get the following increasing/decreasing information for the function.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{Increasing : }}\left[ { - 7, - 1.4454} \right)\,\,\,\,\,\& \,\,\,\,\,\left( {1.4454,4} \right]\hspace{0.25in}\hspace{0.5in}\,\,\,\,\,\,\,\,\,{\mbox{Decreasing : }}\left( { - 1.4454,1.4454} \right)}}\]c Classify the critical points as relative maximums, relative minimums or neither. Show Solution
From the number line in the previous step we get the following classifications of the critical points.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{t = - 1.4454:\,\,\,{\mbox{Relative Maximum}}\hspace{0.5in}\hspace{0.5in}\hspace{0.5in}\,\,\,t = 1.4454:\,\,\,{\mbox{Relative Minimum}}\,}}\]d Determine the intervals on which the function is concave up and concave down. Show Solution
We’ll need the 2nd derivative to find the list of possible inflection points.
\[\underline {Q''\left( t \right) = 2\sin \left( {{\frac{t}{2}}} \right)} \]All possible inflection points of the function are,
\[\begin{array}{*{20}{c}}{t = 4\pi n}\\{t = 2\pi + 4\pi n}\end{array}\hspace{0.5in}\hspace{0.25in}n = 0,\, \pm 1,\, \pm 2,\, \pm 3, \ldots \]Plugging in some values of \(n\) we see that the possible inflection points in the interval \(\left[ { - 7,4} \right]\) are,
\[\underline {t = - 6.2832\hspace{0.5in}\& \hspace{0.5in}\,t = 0} \]To get the intervals of concavity we’ll need the number line for the 2nd derivative.
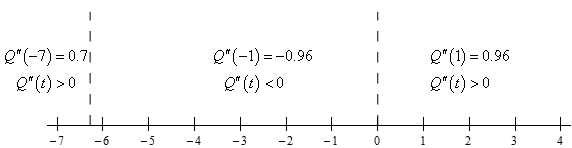
From this we get the following concavity information for the function.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{Concave Up : }}\left[ { - 7, - 6.2832} \right)\,\,\,\,\,\,\& \,\,\,\,\,\,\left( {0,4} \right]\hspace{0.5in}{\mbox{Concave Down : }}\left( { - 6.2832,0} \right)}}\]e Determine the inflection points of the function. Show Solution
From the concavity information in the previous step we can see that the inflection points for the function are,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{t = - 6.2832\hspace{0.5in}\& \,\,\,\,\,\,\,\,t = 0}}\]f Use the information from steps (a) – (e) to sketch the graph of the function. Show Solution
Here is a sketch of the graph of this function using the information above. As we did in problems in this section we can start at the left and work our way to the right on the graph. As we do this we first pay attention to the increasing/decreasing information and then make sure that the curve has the correct concavity as we sketch it in.
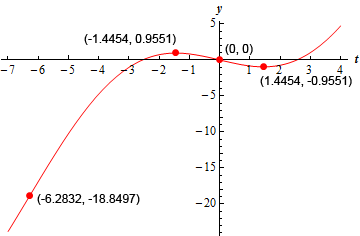
Note that because we used a computer to generate the sketch it is possible that your sketch won’t be quite the same. It should however, have the same points listed on the graph above, the same basic increasing/decreasing nature and the same basic concavity.