Calculus I - The Shape of a Graph, Part II

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 4.6 : The Shape of a Graph, Part II

Back to Problem List

6. For \(h\left( w \right) = 8 - 5w + 2{w^2} - \cos \left( {3w} \right)\) on \(\left[ { - 1,2} \right]\) answer each of the following questions.

Determine a list of possible inflection points for the function.
Determine the intervals on which the function is concave up and concave down.
Determine the inflection points of the function.

Show All Solutions Hide All Solutions

a Determine a list of possible inflection points for the function. Show Solution

To get the list of possible inflection points for the function we’ll need the 2^nd derivative of the function so here that is.

\[h'\left( w \right) = - 5 + 4w + 3\sin \left( {3w} \right)\hspace{0.5in}\underline {h''\left( w \right) = 4 + 9\cos \left( {3w} \right)} \]

Now, recall that possible inflection points are where the 2^nd derivative either doesn’t exist or is zero. Clearly the 2^nd derivative exists everywhere (the cosine function exists everywhere…) and so all we need to do is set the 2^nd derivative equal to zero and solve. We’re not going to show all of those details so if you need to do some review of the process go back to the Solving Trig Equations sections for some examples.

The possible inflection critical points of this function are,

\[\begin{array}{*{20}{c}}{w = 0.6771 + {\textstyle{{2\pi } \over 3}}n}\\{w = 1.4173 + {\textstyle{{2\pi } \over 3}}n}\end{array} \hspace{0.5in}n = 0,\, \pm 1,\, \pm 2,\, \pm 3, \ldots \]

Plugging in some \(n\)’s gives the following possible inflection points in the interval \(\left[ { - 1,2} \right]\).

\[\underline {w = - 0.6771\hspace{0.5in}w = 0.6771\hspace{0.5in}w = 1.4173} \]

b Determine the intervals on which the function is concave up and concave down. Show Solution

There isn’t much to this part. All we really need here is a number line for the 2^nd derivative. Here that is,

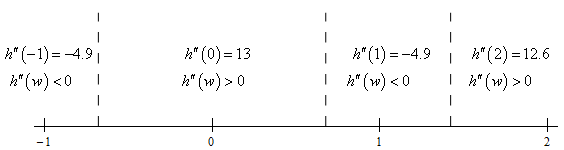
From this we get the following concave up/concave down information for the function.

\[\require{bbox} \bbox[2pt,border:1px solid black]{\begin{align*}\,\,\,\,\,\,\,{\mbox{Concave Up : }} & \left( { - 0.6771,\,\,0.6771} \right)\,\,\,\,\,\& \,\,\,\,\,\left( {1.4173,\,\,2} \right]\\ {\mbox{Concave Down : }} & \left[ { - 1,\,\, - 0.6771} \right)\,\,\,\,\,\,\& \,\,\,\,\,\,\left( {0.6771,\,\,1.4173} \right)\end{align*}}\]

Be careful with the end points of these intervals! We are working on the interval \(\left[ { - 1,2} \right]\) and we’ve done no work for concavity outside of this interval and so we can’t say anything about what happens outside of the interval.

c Determine the inflection points of the function. Show Solution

For this part all we need to do is interpret the results from the previous step. Recall that inflection points are points where the concavity changes (as opposed to simply the points where the 2^nd derivative is zero or doesn’t exist). Therefore, the inflection points for this function are,

\[\require{bbox} \bbox[2pt,border:1px solid black]{{w = - 0.6771\,\,\,\,\,\,\,w = 0.6771\,\,\,\,\,\,\,\,\,\,w = 1.4173}}\]

As with the previous step we have to be careful and recall that we are working on the interval \(\left[ { - 1,2} \right]\). There are infinitely many more possible inflection points and we’ve done no work outside of the interval to determine if they are in fact inflection points!