Section 4.6 : The Shape of a Graph, Part II
8. For \(h\left( x \right) = {{\bf{e}}^{4 - {x^{\,2}}}}\) answer each of the following questions.
- Determine a list of possible inflection points for the function.
- Determine the intervals on which the function is concave up and concave down.
- Determine the inflection points of the function.
Show All Solutions Hide All Solutions
a Determine a list of possible inflection points for the function. Show SolutionTo get the list of possible inflection points for the function we’ll need the 2nd derivative of the function so here that is.
\[h'\left( x \right) = - 2x{{\bf{e}}^{4 - {x^{\,2}}}}\hspace{0.5in}h''\left( x \right) = - 2{{\bf{e}}^{4 - {x^{\,2}}}} + 4{x^2}{{\bf{e}}^{4 - {x^{\,2}}}} = \underline {2{{\bf{e}}^{4 - {x^{\,2}}}}\left( {2{x^2} - 1} \right)} \]Don’t forget to product rule for the 2nd derivative and factoring the exponential out will help a little with the next step.
Now, recall that possible inflection points are where the 2nd derivative either doesn’t exist or is zero. It should be fairly clear that the 2nd derivative exists everywhere (it is a product of two functions that exist everywhere…). We also know that exponentials are never zero and so the 2nd derivative will be zero at the solutions to \(2{x^2} - 1 = 0\)
The possible inflection critical points of this function are then,
\[\underline {x = \pm \frac{1}{\sqrt{2}} = \pm 0.7071} \]b Determine the intervals on which the function is concave up and concave down. Show Solution
There isn’t much to this part. All we really need here is a number line for the 2nd derivative. Here that is,
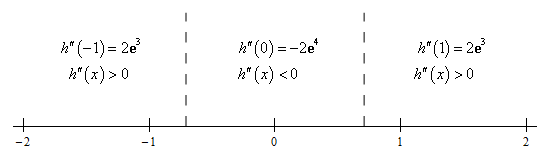
From this we get the following concave up/concave down information for the function.
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\,\,\,\,\,\,\,{\mbox{Concave Up : }}\left( { - \infty , - \frac{1}{\sqrt{2}}} \right)\,\,\,\,\,\& \,\,\,\,\,\left( {\frac{1}{\sqrt{2}},\infty } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,{\mbox{Concave Down : }}\left( { - \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}} \right)}}\]c Determine the inflection points of the function. Show Solution
For this part all we need to do is interpret the results from the previous step. Recall that inflection points are points where the concavity changes (as opposed to simply the points where the 2nd derivative is zero or doesn’t exist). Therefore, the inflection points for this function are,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{x = - \frac{1}{\sqrt{2}} = - 0.7071\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{1}{\sqrt{2}} = 0.7071}}\]