Because we’re dealing with cosine in this problem and we know that the \(x\)-axis represents cosine on a unit circle we’re looking for angles that will have a \(x\) coordinate of \(\frac{1}{2}\). This means we’ll have an angle in the first quadrant and an angle in the fourth quadrant (that we can use the angle in the first quadrant to find). Here is a unit circle for this situation.

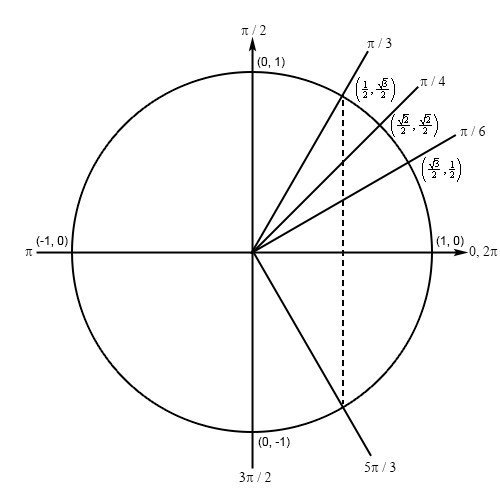
Clearly the angle in the first quadrant is \(\frac{\pi }{3}\) and by some basic symmetry we can see that the terminal line for the second angle must form an angle of \(\frac{\pi }{3}\) with the positive \(x\)-axis as shown above and so it will be : \(2\pi - \frac{\pi }{3} = \frac{{5\pi }}{3}\).

Note that you don’t really need a positive angle for the second one. If you wanted to you could just have easily used \( - \frac{\pi }{3}\) for the second angle. There is nothing wrong with this and you’ll get the same solutions in the end. The reason we chose to go with the positive angle is simply to avoid inadvertently losing the minus sign on the second solution at some point in the future. That kind of mistake is easy to make on occasion and by using positive angles here we will not need to worry about making it.

Show Step 3

From the discussion in the notes for this section we know that once we have these two angles we can get all possible angles by simply adding “\( + \,2\pi n\) for \(n = 0, \pm 1, \pm 2, \ldots \)” onto each of these.

This then means that we must have,

\[\frac{{2x}}{5} = \frac{\pi }{3} + 2\pi n \hspace{0.5in} {\rm{OR }} \hspace{0.5in} \frac{{2x}}{5} = \frac{{5\pi }}{3} + 2\pi n \hspace{0.5in} n = 0, \pm 1, \pm 2, \ldots \]

Finally, to get all the solutions to the equation all we need to do is multiply both sides by \(\frac{5}{2}\).

\[x = \frac{{5\pi }}{6} + 5\pi n \hspace{0.5in} {\rm{OR }} \hspace{0.5in} x = \frac{{25\pi }}{6} + 5\pi n \hspace{0.5in} n = 0, \pm 1, \pm 2, \ldots \] Show Step 4

Note that because at least some of the solutions will have a denominator of 6 it will probably be convenient to also have the interval written in terms of fractions with denominators of 6. Doing this will make it much easier to identify solutions that fall inside the interval so,

\[\left[ {5\pi ,\frac{{40\pi }}{3}} \right] = \left[ {\frac{{30\pi }}{6},\frac{{80\pi }}{6}} \right]\]

With the interval written in this form, if our potential solutions have a denominator of 6, all we need to do is compare numerators. As long as the numerators are between \(30\pi \) and \(80\pi \) we’ll know that the solution is in the interval.

Also, in order to quickly determine the solution for particular values of \(n\) it will be much easier to have both fractions in the solutions have denominators of 6. So the solutions, written in this form, are.

\[x = \frac{{5\pi }}{6} + \frac{{30\pi n}}{6} \hspace{0.5in} {\rm{OR }} \hspace{0.5in} x = \frac{{25\pi }}{6} + \frac{{30\pi n}}{6} \hspace{0.5in} n = 0, \pm 1, \pm 2, \ldots \]

Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of \(n\) we will get negative solutions and these will not be in the interval and so there is no reason to even try these. We can also see from a quick inspection that \(n = 0\) will result in solutions that are not in the interval and so let’s start at \(n = 1\) and see what we get.

\[\begin{array}{llcl}{n = 1:} & {x = \frac{{35\pi }}{6}\,} & {\,\,\,{\rm{OR}}\,\,\,} & {x = \frac{{55\pi }}{6}}\\{n = 2:} & {x = \frac{{65\pi }}{6}\,} & {\,\,\,{\rm{OR}}\,\,\,} & {x = \require{cancel} \xcancel{{\frac{{85\pi }}{{36}}}} > \frac{{80\pi }}{6}}\end{array}\]

There are a couple of things we should note before proceeding. First, it is important to understand both solutions from a given value of \(n\) will not necessarily be in the given interval. It is completely possible, as this problem shows, that we will only get one or the other solution from a given value of \(n\) to fall in the given interval.

Next notice that with each increase in \(n\) we were really just adding another \(\frac{{30\pi }}{6}\) onto the previous results and by a quick inspection we could see that adding \(30\pi \) to the numerator of the first solution from the \(n = 2\) step would result in a numerator that is larger than \(80\pi \) and so would result in a solution that is outside of the interval. Therefore, there was no reason to plug in \(n = 3\) into the first set of solutions. Of course, we also didn’t plug \(n = 3\) into the second set because once we’ve gotten out of the interval adding anything else on will remain out of the interval.

Finally, unlike most of the problems in this section \(n = 0\) did not produce any solutions that were in the given interval. This will happen on occasion so don’t get excited about it when it happens.

So, it looks like we have the three solutions to this equation in the given interval.

\[\require{bbox} \bbox[2pt,border:1px solid black]{{z = \frac{{35\pi }}{6},\,\,\frac{{55\pi }}{6},\,\,\frac{{65\pi }}{6}}}\]