In order to get the solutions it will be much easier to recall the definition of cosecant in terms of sine and rewrite the equation into one involving sine. Doing this gives,

\[\csc \left( {\frac{t}{3}} \right) = \frac{1}{{\sin \left( {\frac{t}{3}} \right)}} = - 9\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\sin \left( {\frac{t}{3}} \right) = - \frac{1}{9}\]

The solution(s) to the equation involving the sine are the same as the solution(s) to the equation involving the cosecant and so working with that will be easier. Using our calculator we can see that,

\[\frac{t}{3} = {\sin ^{ - 1}}\left( { - \frac{1}{9}} \right) = - 0.1113\]

Now we’re dealing with sine in this problem and we know that the \(y\)-axis represents sine on a unit circle and so we’re looking for angles that will have a \(y\) coordinate of \( - \frac{1}{9}\). This means that we’ll have angles in the fourth (this is the one our calculator gave us) and third quadrant. Here is a unit circle for this situation.

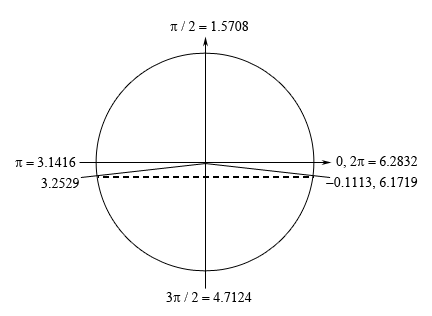
From the symmetry of the unit circle we can see that the second angle will make an angle of 0.1113 with the negative \(x\)-axis and so the second angle will be \(\pi + 0.1113 = 3.2529\). Also, as noted on the unit circle above a positive angle that represents the first angle (i.e. the angle in the fourth quadrant) is \(2\pi - 0.1113 = 6.1719\). We can use either the positive or the negative angle here and we’ll get the same solutions. However, because it is often easy to lose track of minus signs we will be using the positive angle in the fourth quadrant for our work here.

Show Step 3

From the discussion in the notes for this section we know that once we have these two angles we can get all possible angles by simply adding “\( + \,2\pi n\) for \(n = 0, \pm 1, \pm 2, \ldots \)” onto each of these.

This then means that we must have,

\[\frac{t}{3} = 3.2529 + 2\pi n\hspace{0.25in}{\mbox{OR }}\hspace{0.25in}\frac{t}{3} = 6.1719 + 2\pi n\hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \]

Finally, to get all the solutions to the equation all we need to do is multiply both sides by 3 and we’ll convert everything to decimals to help with the final step.

\[\begin{align*}t & = 9.7587 + 6\pi n & \hspace{0.25in}{\mbox{OR }}\hspace{0.25in} & t = 18.5157 + 6\pi n\hspace{0.25in} & n = 0, \pm 1, \pm 2, \ldots \\ & = 9.7587 + 18.8496n & \hspace{0.25in}{\mbox{OR }}\hspace{0.25in} & \hspace{0.10in} = 18.5157 + 18.8496n\hspace{0.25in} & n = 0, \pm 1, \pm 2, \ldots \end{align*}\] Show Step 4

Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of \(n\) we will get negative solutions and these will not be in the interval and so there is no reason to even try these. Also note that even if we start off with \(n = 0\) we will get solutions that are already out of the given interval.

So, despite the fact that there are solutions to this equation none of them fall in the given interval and so there are no solutions to this equation. Do not get excited about the answer here. This kind of situation will happen on occasion and so we need to be aware of it and able to deal with it.