Section 6.4 : Volume With Cylinders
8. Use the method of cylinders to determine the volume of the solid obtained by rotating the region bounded by \(\displaystyle y = \frac{{{{\bf{e}}^{\frac{1}{2}x}}}}{{x + 2}}\), \(\displaystyle y = 5 - \frac{1}{4}x\), \(x = - 1\) and \(x = 6\) about the line \(x = - 2\).
Show All Steps Hide All Steps
We need to start the problem somewhere so let’s start “simple”.
Knowing what the bounded region looks like will definitely help for most of these types of problems since we need to know how all the curves relate to each other when we go to set up the area formula and we’ll need limits for the integral which the graph will often help with.
Here is a sketch of the bounded region with the axis of rotation shown.
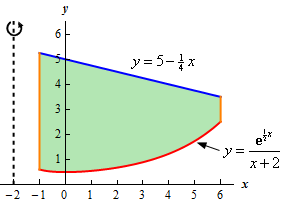
Note that this can be a difficult thing to do especially if you aren’t a very visual person. However, having a representative cylinder can be of great help when we go to write down the area formula. Also, getting the representative cylinder can be difficult without a sketch of the solid of revolution. So, do the best you can at getting these sketches.
Here is a sketch of the solid of revolution.
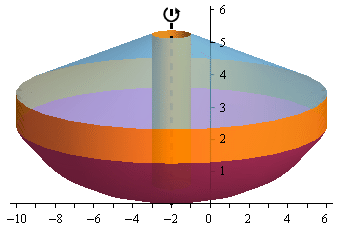
Here are a couple of sketches of a representative cylinder. The image on the left shows a representative cylinder with the front half of the solid cut away and the image on the right shows a representative cylinder with a “wire frame” of the back half of the solid (i.e. the curves representing the edges of the of the back half of the solid).
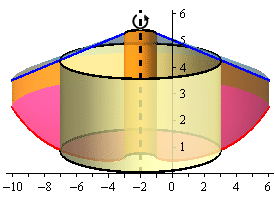
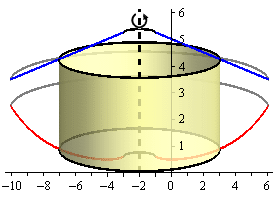
We now need to find a formula for the surface area of the cylinder. Because we are using cylinders that are centered on a vertical axis (i.e. parallel to the \(y\)-axis) we know that the area formula will need to be in terms of \(x\). Therefore, the equations of the curves will need to be in terms of \(x\) (which in this case they already are).
Here is another sketch of a representative cylinder with all of the various quantities we need put into it.
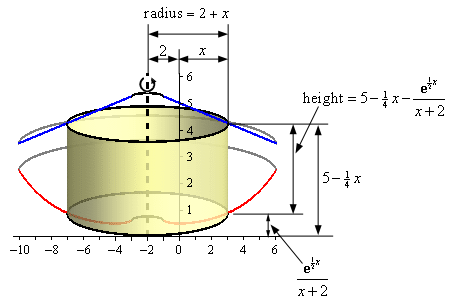
From the sketch we can see the cylinder is centered on the line \(x = - 2\) and the right edge of the cylinder is at some \(x\).
We need to be a little careful with the radius here since the right edge of the cylinder can be on both the left and right side of the \(y\)-axis depending on where it cuts into the solid.
If the right edge of the cylinder cuts into the object to the right of the \(y\)-axis, as shown in the sketch above, then the radius is the distance of the axis of rotation to the \(y\)-axis (a distance of 2) plus the distance from the \(y\)-axis to the right edge of the cylinder (a distance of \(x\)). Therefore, in this case, the radius is \(2 + x\).
On the other hand, if the right edge of the cylinder cuts into the solid to the left of the y‑axis then the radius will be the distance from the axis of rotation to the \(y\)-axis (a distance of 2) minus the distance of the right edge of the cylinder to the \(y\)-axis. However, in this case, the value of the \(x\) that defines the right edge is a negative value and so the distance of the right edge of the cylinder to the \(y\)-axis must be \( - x\). The minus sign in needed to turn this into a positive quantity. Therefore the radius in this case is \(2 - \left( { - x} \right) = 2 + x\), the same as in the first case.
The upper edge of the cylinder is on the curve defining the upper portion of the solid and is a distance of \(5 - \frac{1}{4}x\) from the \(x\)-axis. The lower edge of the cylinder is on the curve defining the lower portion of the solid and is a distance of \(\frac{{{{\bf{e}}^{\frac{1}{2}x}}}}{{x + 2}}\) from the \(x\)-axis. The height then is the difference of these two.
So, the radius and width of the cylinder are,
\[{\mbox{Radius}} = 2 + x\hspace{0.25in}\hspace{0.25in}{\mbox{Width}} = 5 - \frac{1}{4}x - \frac{{{{\bf{e}}^{\frac{1}{2}x}}}}{{x + 2}}\]The area of the cylinder is then,
\[A\left( x \right) = 2\pi \left( {{\mbox{Radius}}} \right)\left( {{\mbox{Height}}} \right) = 2\pi \left( {2 + x} \right)\left( {5 - \frac{1}{4}x - \frac{{{{\bf{e}}^{\frac{1}{2}x}}}}{{x + 2}}} \right) = 2\pi \left( {10 + \frac{9}{2}x - \frac{1}{4}{x^2} - {{\bf{e}}^{\frac{1}{2}x}}} \right)\] Show Step 4The final step is to then set up the integral for the volume and evaluate it.
From the graph from Step 1 we can see that the “first” cylinder in the solid would occur at \(x = - 1\) and the “last” cylinder would occur at \(x = 6\). Our limits are then : \( - 1 \le x \le 6\).
The volume is then,
\[\begin{align*}V & = \int_{{ - 1}}^{6}{{2\pi \left( {10 + \frac{9}{2}x - \frac{1}{4}{x^2} - {{\bf{e}}^{\frac{1}{2}x}}} \right)\,dx}}\\ & = 2\left. {\pi \left( {10x + \frac{9}{4}{x^2} - \frac{1}{{12}}{x^3} - 2{{\bf{e}}^{\frac{1}{2}x}}} \right)} \right|_{ - 1}^6 = \require{bbox} \bbox[2pt,border:1px solid black]{{2\pi \left( {\frac{{392}}{3} + 2{{\bf{e}}^{ - \,\,\frac{1}{2}}} - 2{{\bf{e}}^3}} \right)}}\end{align*}\]