Section 6.6 : Work
4. A tank of water is 15 feet long and has a cross section in the shape of an equilateral triangle with sides 2 feet long (point of the triangle points directly down). The tank is filled with water to a depth of 9 inches. Determine the amount of work needed to pump all of the water to the top of the tank. Assume that the density of the water is 62 lb/ft3.
Show All Steps Hide All Steps
Use the last example from this section as a general guide for this problem if you are having trouble. This problem will work in pretty much the same manner, although there will be some differences due to the obvious change in tank shape as well as the fact that we are using not using the Metric system for this problem.
Okay, let’s start off and define \(x = 0\) to be the bottom point of the tank and the height of the water in the tank to be \(x = \frac{9}{{12}} = \frac{3}{4}\) feet (because all the other quantities are in feet we converted this into feet as well). This means that we will be working in the interval \(\left[ {0,\frac{3}{4}} \right]\) for this problem.
We’ll next divide the interval \(\left[ {0,\frac{3}{4}} \right]\) into \(n\) subintervals each of width \(\Delta x\) and we’ll let \(x_i^*\) be any point in the \(i\)th subinterval where \(n = 1,2, \ldots ,n\). For each subinterval we can approximate the water in the tank corresponding to that subinterval as a box with length 15 ft, width \(s_i^*\) and height \(\Delta x\).
Here is a quick sketch of the tank. The red strip represents the box we are using to approximate the water in the tank in the \(i\)th subinterval.
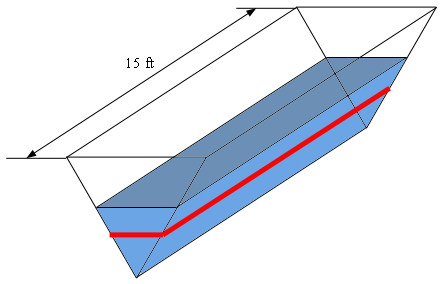
The sketch of the tank is nice and while it does help us to visualize the tank what we really need is a sketch of the tank from directly in front (i.e. a typical vertical equilateral triangular cross‑section for the tank). Here is that sketch.
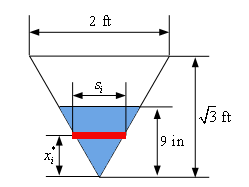
The red strip again represents the box we are using to approximate the water in the \(i\)th subinterval. As noted in the problem statement the cross-section is an equilateral triangle and with sides of length 2 feet.
We included the height in the above sketch and this is easy to get using some basic right triangle trig. Here is yet another sketch of the cross-section.
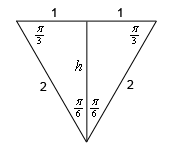
Because the triangle is an equilateral triangle we know that each of the interior angles of the triangle must be \(\frac{\pi }{3}\) and we’re told the length of each side is 2. The height of the triangle is the line that bisects the triangle as shown. Each half of the triangle is then an identical right triangle and using any of the trig functions we can quickly determine the height of the triangle. We’ll use cosine here.
\[\cos \left( {\frac{\pi }{6}} \right) = \frac{h}{2}\hspace{0.25in} \Rightarrow \hspace{0.25in}h = 2\cos \left( {\frac{\pi }{6}} \right) = \sqrt 3 \]We’ll next need the volume of the box of water we using to approximate the volume of water in the \(i\)th subinterval (as represented by the red strip in the first two pictures from Step 1).
Our approximate volume is the volume of a box and so we know that the volume for the \(i\)th subinterval would be,
\[{V_i} = \left( \mbox{length} \right)\left( \mbox{width} \right)\left( \mbox{height} \right) = \left( {15} \right)\left( {{s_i}} \right)\left( {\Delta x} \right) = 15\,{s_i}\,\Delta x\]We will eventually need the volume to be in terms of \(x_i^*\) and luckily enough this is easy enough to do.
From the cross-section sketch with the red strip in Step 1 we see that we have two similar triangles (well actually we have three but we only need two of them). The two that we need are the triangle with width 2 and height \(\sqrt 3 \) and the triangle whose width is \({s_i}\) (i.e. the triangle whose top is the red strip) and whose height is \(x_i^*\). Since these two triangles are similar we now the following two ratios must be equal.
\[\frac{{{s_i}}}{{x_i^*}} = \frac{2}{{\sqrt 3 }}\hspace{0.25in} \Rightarrow \hspace{0.25in} {s_i} = \frac{2}{{\sqrt 3 }}x_i^*\]Plugging this into the volume formula above and we get,
\[{V_i} = \frac{{30}}{{\sqrt 3 }}x_i^*\,\Delta x\]Note that because we are working with the Imperial system here the force in this case is just \({F_i} = {\mbox{density}} \times {V_i}\).
We next need to know how much force will be required to overcome the force of gravity that is acting on the water in the \(i\)th subinterval. This will be approximately the forced needed to overcome the force of gravity acting on the volume of water we found in Step 2. Because we are working with the British system here the force is,
\[{F_i} = {\mbox{density}} \times {V_i} \approx \left( {62} \right)\left( {\frac{{30}}{{\sqrt 3 }}x_i^*\,\Delta x} \right) = \frac{{1860}}{{\sqrt 3 }}x_i^*\,\Delta x\]We will need the amount of work required to raise the volume of water in the \(i\)th subinterval to the top of the tank, i.e. raise it a distance of \(\sqrt 3 - x_i^*\). This is approximately,
\[{W_i} \approx {F_i}\left( {\sqrt 3 - x_i^*} \right) = \frac{{1860}}{{\sqrt 3 }}x_i^*\left( {\sqrt 3 - x_i^*} \right)\Delta x\]The total amount of work to raise all the water to the top of the tank is the approximately the sum of all the \({W_i}\) for \(i = 1,2, \ldots n\) or,
\[W \approx \sum\limits_{i = 1}^n {\frac{{1860}}{{\sqrt 3 }}x_i^*\left( {\sqrt 3 - x_i^*} \right)\Delta x} \]The exact work required is then found by letting \(n \to \infty \) or,
\[W = \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {\frac{{1860}}{{\sqrt 3 }}x_i^*\left( {\sqrt 3 - x_i^*} \right)\Delta x} \]This however is just the definition of the following definite integral,
\[W = \int_{0}^{{\frac{3}{4}}}{{\frac{{1860}}{{\sqrt 3 }}x\left( {\sqrt 3 - x} \right)\,dx}}\]The work required to pump all the water to the top of the tank is then,
\[W = \int_{0}^{{\frac{3}{4}}}{{\frac{{1860}}{{\sqrt 3 }}x\left( {\sqrt 3 - x} \right)\,dx}} = \left. {\frac{{1860}}{{\sqrt 3 }}\left( {\frac{{\sqrt 3 }}{2}\,{x^2} - \frac{1}{3}{x^3}} \right)} \right|_0^{\frac{3}{4}} = \require{bbox} \bbox[2pt,border:1px solid black]{{{\mbox{372}}{\mbox{.112 ft - lbs}}}}\]