I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 12.5 : Functions of Several Variables
4. Find the domain of the following function.
\[f\left( {x,y} \right) = \frac{1}{x} + \sqrt {y + 4} - \sqrt {x + 1} \] Show SolutionThere really isn’t all that much to this problem. We know that we can’t have division by zero and we can’t take square roots of negative numbers and so we’ll need to require that whatever \(\left( {x,y} \right)\) is it will need to satisfy the following three conditions.
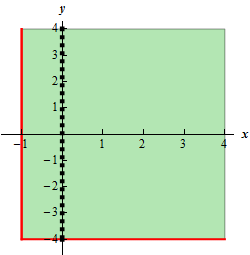
\[x \ge - 1\hspace{0.5in}x \ne 0\hspace{0.5in}y \ge - 4\]This is also our domain since these are the only conditions require in order for the function to exist.
A sketch of the domain is shown below. We can take any point in the green area or on the red lines with the exception of the \(y\)-axis (i.e. \(x \ne 0\)) as indicated by the black dashes on the \(y\)-axis.