Section 9.1 : Parametric Equations and Curves
1. Eliminate the parameter for the following set of parametric equations, sketch the graph of the parametric curve and give any limits that might exist on \(x\) and \(y\).
\[x = 4 - 2t\hspace{0.5in}y = 3 + 6t - 4{t^2}\]Show All Steps Hide All Steps
Start SolutionFirst, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations we can do that by solving the \(x\) equation for \(t\) and plugging that into the \(y\) equation.
Doing that gives (we’ll leave it to you to verify all the algebra bits…),
\[t = \frac{1}{2}\left( {4 - x} \right)\hspace{0.5in}\,\, \to \hspace{0.5in}\,\,\,y = 3 + 6\left[ {\frac{1}{2}\left( {4 - x} \right)} \right] - 4{\left[ {\frac{1}{2}\left( {4 - x} \right)} \right]^2} = - {x^2} + 5x - 1\] Show Step 2Okay, from this it looks like we have a parabola that opens downward. To sketch the graph of this we’ll need the \(x\)-intercepts, \(y\)-intercept and most importantly the vertex.
For notational purposes let’s define \(f\left( x \right) = - {x^2} + 5x - 1\).
The \(x\)-intercepts are then found by solving \(f\left( x \right) = 0\). Doing this gives,
\[ - {x^2} + 5x - 1 = 0\hspace{0.5in}\,\,\,\, \to \hspace{0.5in}\,\,\,x = \frac{{ - 5 \pm \sqrt {{{\left( 5 \right)}^2} - 4\left( { - 1} \right)\left( { - 1} \right)} }}{{2\left( { - 1} \right)}} = \frac{{5 \pm \sqrt {21} }}{2} = 0.2087,\,\,\,4.7913\]The \(y\)-intercept is : \(\left( {0,f\left( 0 \right)} \right) = \left( {0, - 1} \right)\).
Finally, the vertex is,
\[\left( { - \frac{b}{{2a}},f\left( { - \frac{b}{{2a}}} \right)} \right) = \left( {\frac{{ - 5}}{{2\left( { - 1} \right)}},f\left( {\frac{5}{2}} \right)} \right) = \left( {\frac{5}{2},\frac{{21}}{4}} \right)\] Show Step 3Before we sketch the graph of the parametric curve recall that all parametric curves have a direction of motion, i.e. the direction indicating increasing values of the parameter, \(t\) in this case.
There are several ways to get the direction of motion for the curve. One is to plug in values of \(t\) into the parametric equations to get some points that we can use to identify the direction of motion.
Here is a table of values for this set of parametric equations.
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| -1 | 6 | -7 |
| 0 | 4 | 3 |
| \(\frac{3}{4}\) | \(\frac{5}{2}\) | \(\frac{{21}}{4}\) |
| 1 | 2 | 5 |
| 2 | 0 | -1 |
| 3 | -2 | -15 |
Note that \(t = \frac{3}{4}\) is the value of \(t\) that give the vertex of the parabola and is not an obvious value of \(t\) to use! In fact, this is a good example of why just using values of \(t\) to sketch the graph is such a bad way of getting the sketch of a parametric curve. It is often very difficult to determine a good set of \(t\)’s to use.
For this table we first found the vertex \(t\) by using the fact that we actually knew the coordinates of the vertex (the \(x\)-coordinate for this example was the important one) as follows,
\[x = \frac{5}{2}\,\,\,\,:\,\,\,\,\,\frac{5}{2} = 4 - 2t\hspace{0.5in} \to \hspace{0.5in}\,\,t = \frac{3}{4}\]Once this value of \(t\) was found we chose several values of \(t\) to either side for a good representation of \(t\) for our sketch.
Note that, for this case, we used the \(x\)-coordinates to find the value of the \(t\) that corresponds to the vertex because this equation was a linear equation and there would be only one solution for \(t\). Had we used the \(y\)‑coordinate we would have had to solve a quadratic (not hard to do of course) that would have resulted in two \(t\)’s. The problem is that only one \(t\) gives the vertex for this problem and so we’d need to then check them in the \(x\) equation to determine the correct one. So, in this case we might as well just go with the \(x\) equation from the start.
Also note that there is an easier way (probably – it will depend on you of course) to determine direction of motion. Take a quick look at the \(x\) equation.
\[x = 4 - 2t\]Because of the minus sign in front of the \(t\) we can see that as \(t\) increases \(x\) must decrease (we can verify with a quick derivative/Calculus I analysis if we want to). This means that the graph must be tracing out from right to left as the table of values above in the table also indicates.
Using a quick Calculus analysis of one, or both, of the parametric equations is often a better and easier method for determining the direction of motion for a parametric curve. For “simple” parametric equations we can often get the direction based on a quick glance at the parametric equations and it avoids having to pick “nice” values of \(t\) for a table.
Show Step 4We could sketch the graph at this point, but let’s first get any limits on \(x\) and \(y\) that might exist.
Because we have a parabola that opens downward and we’ve not restricted \(t\)’s in any way we know that we’ll get the whole parabola. This in turn means that we won’t have any limits at all on \(x\) but \(y\) must satisfy \(y \le \frac{{21}}{4}\) (remember the \(y\)-coordinate of the vertex?).
So, formally here are the limits on \(x\) and \(y\).
\[ - \infty < x < \infty \hspace{0.25in}\hspace{0.25in}y \le \frac{{21}}{4}\]Note that having the limits on \(x\) and \(y\) will often help with the actual graphing step so it’s often best to get them prior to sketching the graph. In this case they don’t really help as we can sketch the graph of a parabola without these limits, but it’s just good habit to be in so we did them first anyway.
Show Step 5Finally, here is a sketch of the parametric curve for this set of parametric equations.
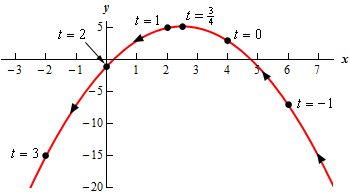
For this sketch we included the points from our table because we had them but we won’t always include them as we are often only interested in the sketch itself and the direction of motion.