Section 9.1 : Parametric Equations and Curves
11.The path of a particle is given by the following set of parametric equations. Completely describe the path of the particle. To completely describe the path of the particle you will need to provide the following information.
- A sketch of the parametric curve (including direction of motion) based on the equation you get by eliminating the parameter.
- Limits on \(x\) and \(y\).
- A range of \(t\)’s for a single trace of the parametric curve.
- The number of traces of the curve the particle makes if an overall range of \(t\)’s is provided in the problem.
Show All Steps Hide All Steps
Start SolutionThere’s a lot of information we’ll need to find to fully answer this problem. However, for most of it we can follow the same basic ordering of steps we used for the first few problems in this section. We will need however to do a little extra work along the way.
Also, because most of the work here is similar to the work we did in Problems 4 – 6 of this section we won’t be putting in as much explanation to a lot of the work we’re doing here. So, if you need some explanation for some of the work you should go back to those problems and check the corresponding steps.
First, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations let’s first notice that we can solve the \(x\) equation for the exponential function as follows,
\[{{\bf{e}}^{ - 3t}} = 2x\]Now, just recall that \({{\bf{e}}^{ - 6t}} = {\left( {{{\bf{e}}^{ - 3t}}} \right)^2}\) and so we can plug the above equation into the exponential in the \(y\) equation to get,
\[\,y = {{\bf{e}}^{ - 6t}} + 2{{\bf{e}}^{ - 3t}} - 8 = {\left( {{{\bf{e}}^{ - 3t}}} \right)^2} + 2{{\bf{e}}^{ - 3t}} - 8 = {\left( {2x} \right)^2} + 2\left( {2x} \right) - 8 = 4{x^2} + 4x - 8\]So, the parametric curve will be some or all of the graph of this quadratic function.
Show Step 2At this point let’s work on the limits for \(x\) and \(y\). In this case, unlike most of the previous problems, things will work a little differently.
Let’s start by noting that unlike sine and cosine functions we know \({{\bf{e}}^{ - 3t}}\) is always a decreasing function as \(t\) increases (you can do some quick Calculus I work to verify this right?).
Why do we care about this? Well first the \(x\) equation is just a constant times \({{\bf{e}}^{ - 3t}}\) and so the fact that \({{\bf{e}}^{ - 3t}}\) is a decreasing function means that the \(x\) equation, \(x = \frac{1}{2}{{\bf{e}}^{ - 3t}}\), is also a decreasing function (because the coefficient is positive).
Next, we aren’t given a range of \(t\)’s for this problem and so we can assume the largest possible range of \(t\)’s. Therefore, we are safe in assuming a range of \( - \infty < t < \infty \) for the \(t\)’s.
Now, as we’ve already noted the know that the \(x\) equation is decreasing and so the largest value of \(x\) will occur at the left “end point” of the range. Likewise, the smallest value of \(x\) will occur at the right “end point” of the range. For this problem both “end points” of our range are in fact infinities so we can’t just plug in as we did in the previous problem. We can however take the following two limits.
\[\mathop {\lim }\limits_{t \to \,\, - \,\infty } \left( {\frac{1}{2}{{\bf{e}}^{ - 3t}}} \right) = \infty \hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\mathop {\lim }\limits_{t \to \,\,\,\infty } \left( {\frac{1}{2}{{\bf{e}}^{ - 3t}}} \right) = 0\]From this we can see that as we approach the left end point of the \(t\) range the value of \(x\) is going to infinity and as we approach the right end point of the \(t\) range the \(x\) value is going to zero. Note however that \(x\) can never actually be zero because \(x\) is still defined in terms of an exponential function (which can’t be zero). All the limit is telling us is that as we let \(t \to \infty \) we will get \(x \to 0\).
The range of \(x\) for our parametric curve is therefore,
\[0 < x < \infty \]Again, be careful with the inequalities here! We know that \(x\) can be neither zero nor infinity so we must use strict inequalities for this range. This is something that we always need to be on the lookout for with variable ranges of parametric equations. Depending on the parametric equations sometimes the end points of the ranges will be strict inequalities (as with this problem) and for others they include the end points (as with the previous problems).
For the range of \(y\)’s we will need to do a little work to get the correct range of \(y\)’s but it won’t be as much extra work as in previous problems and we can do it all in this step. Let’s just sketch the graph and see what we get. Here is a quick sketch of the graph.
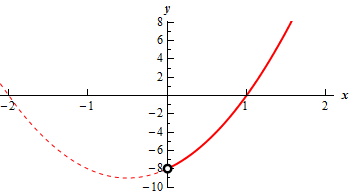
The dotted portion of the graph is full graph of the function on \( - 2 \le t \le 2\) without regards to the actual restriction on \(x\). The solid portion of the graph is the portion of the graph that corresponds to the restriction on \(x\) that we found earlier in this step.
Note the “open dot” on the \(y\)-axis for the left end of the graph. This needs to be here to acknowledge that \(x \ne 0\). We can also see that the \(y\) value at this point is \(y = - 8\) and again we can see that for the parametric curve we have \(y \ne - 8\).
Also, keep in mind that we know that \(x \to \infty \) and so we also know that the \(y\) portion of the graph must also continue up to infinity to match the \(x\) behavior.
So, from this quick analysis of the graph we can see that the \(y\) range for the parametric curve must be,
\[ - 8 < y < \infty \] Show Step 3We now need to do the direction of motion for this curve but note that we actually found the direction of motion in the previous step.
As noted in the previous step we know that \(x = \frac{1}{2}{{\bf{e}}^{ - 3t}}\) is a decreasing function and so the \(x\)’s must be decreasing as \(t\) increases. Therefore, the equation must be moving from right to left as the curve is traced out.
Also note that unlike most of the previous problems we know that no portion of the graph will be retraced. Again, we know the \(x\) equation is a decreasing equation. If the curve were to retrace any portion we can see that the only way to do that would be to move back from left to right which would require \(x\) to increase and that can’t happen.
This means that we now know as well that the graph will trace out exactly once.
Show Step 4Now that we have all the needed information we can do a formal sketch of the graph.
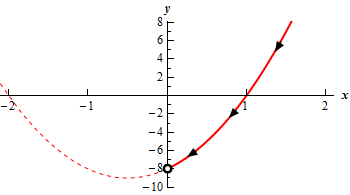
As with the graph above the dotted portion of the graph is full graph of the function on \( - 2 \le t \le 2\) and the solid portion of the graph is the portion that corresponds to the restrictions \(x\) and \(y\) we found in Step 2.
Here is also the formal answers for all the rest of the information that problem asked for.
\[\begin{array}{lcc}{\mbox{Range of }}x{\mbox{ :}} & \hspace{0.1in} & 0 < x < \infty \\ {\mbox{Range of }}y{\mbox{ :}} & \hspace{0.1in} & - 8 < y < \infty \\ {\mbox{Range of }}t{\mbox{ for one trace : }} & \hspace{0.1in} & - \infty < t < \infty \\ {\mbox{Total number of traces : }} & \hspace{0.1in} & 1\end{array}\]