Section 9.1 : Parametric Equations and Curves
7.The path of a particle is given by the following set of parametric equations. Completely describe the path of the particle. To completely describe the path of the particle you will need to provide the following information.
- A sketch of the parametric curve (including direction of motion) based on the equation you get by eliminating the parameter.
- Limits on \(x\) and \(y\).
- A range of \(t\)’s for a single trace of the parametric curve.
- The number of traces of the curve the particle makes if an overall range of \(t\)’s is provided in the problem.
Show All Steps Hide All Steps
Start SolutionThere’s a lot of information we’ll need to find to fully answer this problem. However, for most of it we can follow the same basic ordering of steps we used for the first few problems in this section. We will need however to do a little extra work along the way.
Also, because most of the work here is similar to the work we did in Problems 4 – 6 of this section we won’t be putting in as much explanation to a lot of the work we’re doing here. So, if you need some explanation for some of the work you should go back to those problems and check the corresponding steps.
First, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations we will make use of the well-known trig identity,
\[{\cos ^2}\left( \theta \right) + {\sin ^2}\left( \theta \right) = 1\]We can solve each of the parametric equations for sine and cosine as follows,
\[\cos \left( {3t} \right) = \frac{{x - 3}}{{ - 2}}\hspace{0.25in}\hspace{0.25in}\sin \left( {3t} \right) = \frac{{y - 1}}{4}\]Plugging these into the trig identity gives,
\[{\left( {\frac{{x - 3}}{{ - 2}}} \right)^2} + {\left( {\frac{{y - 1}}{4}} \right)^2} = 1\hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}\frac{{{{\left( {x - 3} \right)}^2}}}{4} + \frac{{{{\left( {y - 1} \right)}^2}}}{{16}} = 1\]Therefore, the parametric curve will be some or all of the graph of this ellipse.
Show Step 2At this point let’s get our first guess as to the limits on \(x\) and \(y\). As noted in previous problems what we’re really finding here is the largest possible ranges for \(x\) and \(y\). In later steps we’ll determine if this the actual set of limits on \(x\) and \(y\) or if we have smaller ranges.
We can use our knowledge of sine and cosine to determine the limits on \(x\) and \(y\) as follows,
\[\begin{array}{c} - 1 \le \cos \left( {3t} \right) \le 1 & \hspace{1.0in} & - 1 \le \sin \left( {3t} \right) \le 1\\ 2 \ge - 2\cos \left( {3t} \right) \ge - 2& \hspace{1.0in} & - 4 \le 4\sin \left( {3t} \right) \le 4\\ 5 \ge 3 - 2\cos \left( {3t} \right) \ge 1 & \hspace{1.0in} & - 3 \le 1 + 4\sin \left( {3t} \right) \le 5\\ 1 \le x \le 5 & \hspace{1.0in} & - 3 \le y \le 5\end{array}\]Remember that all we need to do is start with the appropriate trig function and then build up the equation for \(x\) and \(y\) by first multiplying the trig function by any coefficient, if present, and then adding/subtracting any numbers that might be present. We now have the largest possible set of limits for \(x\) and \(y\).
This problem does not have a range of \(t\)’s that might restrict how much of the parametric curve gets sketched out. This means that the parametric curve will be fully traced out.
Remember that when we talk about the parametric curve getting fully traced out this doesn’t, in general, mean the full ellipse we found in Step 1 gets traced out by the parametric equation. All “fully traced out” means, in general, is that whatever portion of the ellipse that is described by the set of parametric curves will be completely traced out.
However, for this problem let’s also note as well that the ranges for \(x\) and \(y\) we found above also correspond the maximum ranges for \(x\) and \(y\) we get from the equation of the ellipse we found in Step 1. This means that, for this problem, the ellipse will get fully traced out at least once by the parametric curve and so these are the full limits on \(x\) and \(y\).
Show Step 3Let’s next get the direction of motion for the parametric curve.
Let’s use \(t = 0\) as a “starting” point for this analysis. At \(t = 0\) we are at the point \(\left( {1,1} \right)\). If we increase \(t\) we can see that both \(x\) and \(y\) must increase until we get to the point \(\left( {3,5} \right)\). Increasing \(t\) further from this point will force \(x\) to continue to increase, but \(y\) will now start to decrease until we reach the point \(\left( {5,1} \right)\). Next, when we increase \(t\) further both \(x\) and \(y\) will decrease until we reach the point \(\left( {3, - 3} \right)\). Finally, increasing \(t\) even more we get \(x\) continuing to decrease while \(y\) starts to increase until we get back to \(\left( {1,1} \right)\), the point we “started” the analysis at.
We didn’t put a lot of “explanation into this but if you think about the parametric equations and how sine/cosine behave as you increase \(t\) you should see what’s going on. In the \(x\) equation we see that the coefficient of the cosine is negative and so if cosine increases \(x\) must decrease and if cosine decreases \(x\) must increase. For the \(y\) equation the coefficient of the sine is positive and so both \(y\) and sine will increase or decrease at the same time.
Okay, in all of the analysis above we must be moving in a clockwise direction. Also, note that because of the oscillating nature of sine and cosine once we reach back to the “starting” point the behavior will simply repeat itself. This in turn tells us that once we arrive back at the “starting” point we will continue to trace out the parametric curve in a clockwise direction.
Show Step 4From the analysis in the last step we saw that without any range of \(t\)’s restricting the parametric curve, which we don’t have here, the parametric curve will completely trace out the ellipse that we found in Step 1.
Therefore, the next thing we should do is determine a range of \(t\)’s that it will take to complete one trace of the parametric curve. Note that one trace of the parametric curve means that no portion of the parametric curve will ever be retraced. For this problem that means we trace out the ellipse exactly once.
So, as with the last step let’s “start” at the point \(\left( {1,1} \right)\), which corresponds to \(t = 0\). So, the next question to ask is what value of \(t > 0\) will we reach this point again.
In order to be at the point \(\left( {1,1} \right)\) we need to require that \(\cos \left( {3t} \right) = 1\) and \(\sin \left( {3t} \right) = 0\). So, for \(t > 0\) we know we’ll have \(\cos \left( {3t} \right) = 1\) if \(3t = 2\pi ,4\pi ,6\pi , \ldots \) and we’ll have \(\sin \left( {3t} \right) = 0\) if \(3t = \pi ,2\pi ,3\pi , \ldots \) .
The first value of \(t\) that is in both of these lists is \(3t = 2\pi \). So, we’ll get back to the “starting” point at,
\[3t = 2\pi \hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}t = \frac{{2\pi }}{3}\]Therefore, one trace will be completed in the range,
\[0 \le t \le \frac{{2\pi }}{3}\]Note that this is only one possible answer here. Any range of \(t\)’s with a “net” range of \(\frac{{2\pi }}{3}\) \(t\)’s, with the endpoints of the \(t\) range corresponding to start/end points of the parametric equation, will work. So, for example, any of the following ranges of \(t\)’s would also work.
\[ - \frac{{2\pi }}{3} \le t \le 0\hspace{0.25in}\hspace{0.25in}\frac{{2\pi }}{3} \le t \le \frac{{4\pi }}{3}\hspace{0.25in}\hspace{0.25in} - \frac{\pi }{3} \le t \le \frac{\pi }{3}\]There are of course many other possible ranges of \(t\)’s for a one trace. Note however, as the last example above shows, because the full ellipse is traced out, each range doesn’t all need to start/end at the same place. The range we originally arrived at as well as the first two ranges above all start/end at \(\left( {1,1} \right)\) while the third range above starts/ends at \(\left( {5,1} \right)\).
Show Step 5Now that we have a range of \(t\)’s for one full trace of the parametric curve we could determine the number of traces the particle makes. However, because we weren’t given an overall range of \(t\)’s we can’t do that for this problem.
Show Step 6Finally, here is a sketch of the parametric curve for this set of parametric equations.
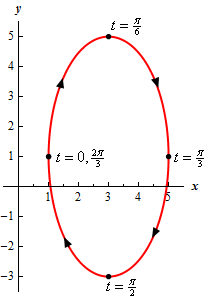
For this sketch we included a set of \(t\)’s to illustrate where the particle is at while tracing out of the curve. For some practice you might want to follow the analysis from Step 4 to see if you can verify the values of \(t\) for the other three points on the graph. It would, of course, be easier to just plug them in to verify, but the practice would of the Step 4 analysis might be useful to you.
Here is also the formal answers for all the rest of the information that problem asked for.
\[\begin{array}{lcc} {\mbox{Range of }}x{\mbox{ :}} & \hspace{0.1in} & 1 \le x \le 5\\ {\mbox{Range of }}y{\mbox{ :}} & \hspace{0.1in} & - 3 \le y \le 5\\ {\mbox{Range of }}t{\mbox{ for one trace : }} & \hspace{0.1in} & 0 \le t \le \frac{{2\pi }}{3}\\ {\mbox{Total number of traces : }} & \hspace{0.1in} & {\mbox{n/a}}\end{array}\]