Section 9.1 : Parametric Equations and Curves
9.The path of a particle is given by the following set of parametric equations. Completely describe the path of the particle. To completely describe the path of the particle you will need to provide the following information.
- A sketch of the parametric curve (including direction of motion) based on the equation you get by eliminating the parameter.
- Limits on \(x\) and \(y\).
- A range of \(t\)’s for a single trace of the parametric curve.
- The number of traces of the curve the particle makes if an overall range of \(t\)’s is provided in the problem.
Show All Steps Hide All Steps
Start SolutionThere’s a lot of information we’ll need to find to fully answer this problem. However, for most of it we can follow the same basic ordering of steps we used for the first few problems in this section. We will need however to do a little extra work along the way.
Also, because most of the work here is similar to the work we did in Problems 4 – 6 of this section we won’t be putting in as much explanation to a lot of the work we’re doing here. So, if you need some explanation for some of the work you should go back to those problems and check the corresponding steps.
First, we’ll eliminate the parameter from this set of parametric equations. For this particular set of parametric equations notice that we can quickly and easily eliminate the parameter simply by solving the \(y\) equation for cosine as follows,
\[\cos \left( {\frac{5}{2}t} \right) = 3y - 3\]Plugging this into the cosine in the \(x\) equation gives,
\[x = \sqrt {4 + \left( {3y - 3} \right)} \hspace{0.25in}\hspace{0.25in} \Rightarrow \hspace{0.25in}\hspace{0.25in}x = \sqrt {1 + 3y} \]So, the parametric curve will be some or all of the graph of this square root function.
Show Step 2At this point let’s get our first guess as to the limits on \(x\) and \(y\). As noted in previous problems what we’re really finding here is the largest possible ranges for \(x\) and \(y\). In later steps we’ll determine if this the actual set of limits on \(x\) and \(y\) or if we have smaller ranges.
We can use our knowledge of cosine to determine the limits on \(x\) and \(y\) as follows,
\[\begin{array}{c} - 1 \le \cos \left( {\frac{5}{2}t} \right) \le 1 & \hspace{1.0in} & - 1 \le \cos \left( {\frac{5}{2}t} \right) \le 1\\ 3 \le 4 + \cos \left( {\frac{5}{2}t} \right) \le 5 & \hspace{1.0in} & - \frac{1}{3} \le \frac{1}{3}\cos \left( {\frac{5}{2}t} \right) \le \frac{1}{3}\\ \sqrt 3 \le \sqrt {4 + \cos \left( {\frac{5}{2}t} \right)} \le \sqrt 5 & \hspace{1.0in} & \frac{2}{3} \le 1 + \frac{1}{3}\cos \left( {\frac{5}{2}t} \right) \le \frac{4}{3}\\ \sqrt 3 \le x \le \sqrt 5 & \hspace{1.0in} & \frac{2}{3} \le y \le \frac{4}{3}\end{array}\]Remember that all we need to do is start with the cosine and then build up the equation for \(x\) and \(y\) by first multiplying the trig function by any coefficient, if present, and then adding/subtracting any numbers that might be present. We now have the largest possible set of limits for \(x\) and \(y\).
Now, at this point we need to be a little careful. As noted above what we’ve actually found here are the largest possible ranges for the limits on \(x\) and \(y\). This set of inequalities for the limits on \(x\) and \(y\) assume that the parametric curve will be fully traced out at least once for the range of \(t\)’s we were given in the problem statement. It is always possible that the parametric curve will not trace out a full trace in the given range of \(t\)’s. In a later step we’ll determine if the parametric curve does trace out a full trace and hence determine the actual limits on \(x\) and \(y\).
Remember that when we talk about the parametric curve getting fully traced out this doesn’t, in general, mean the full square root graph we found in Step 1 gets traced out by the parametric equation. All “fully traced out” means, in general, is that whatever portion of the square root graph that is described by the set of parametric curves will be completely traced out.
In fact, for this problem, we can see that the square root from Step 1 will not get fully traced out by the particle regardless of any range of \(t\)’s. The largest possible portion of the square root graph that can be traced out by the particle is the portion that lies in the range of \(x\) and \(y\) given above. In a later step we’ll determine if the largest possible portion of the square root graph does get traced out or if the particle only traces out part of it.
Show Step 3Let’s next get the direction of motion for the parametric curve. For this analysis it might be useful to have a quick sketch of the largest possible parametric curve. So, here is a quick sketch of that.
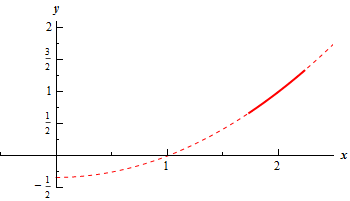
The dashed line is the graph of the full square root from Step 1 and the solid line is the portion that falls into our largest possible range of \(x\) and \(y\) we found in Step 2. As an aside here note that the two ranges are complimentary. In other words, if we sketch the graph only for the range of \(x\) we automatically get the range for \(y\). Likewise, if we sketch the graph only for the range of y we automatically get the range for \(x\). This is a good check for your graph. The \(x\) and \(y\) ranges should always match up!
Before moving on let’s address the fact that is doesn’t look like square root graphs that most of us are used to seeing. Keep in mind that the typical square root function that we’re used to working at is in the form \(y = \sqrt x \). Our equation for this problem however is in the form \(x = \sqrt y \). If you think about it the graph of \(x = \sqrt y \) is nothing more than the portion of the graph of \(y = {x^2}\) corresponding to \(x \ge 0\) (recall square roots only return positive or zero values!). Of course the function for this problem is not \(x = \sqrt y \) but it is similar enough that the ideas discussed here are still valid just for a slightly different function.
Okay, let’s get back to the problem.
This problem is going to be a lot like the previous problem in terms of direction of motion. First note that if we start at the lower left hand point we need to require that \(\cos \left( {\frac{5}{2}t} \right) = - 1\) since that is the only way for both \(x\) and \(y\) to have their minimal values (which puts us at the lower left-hand point)! It also doesn’t matter what value of \(t\) we use at this point. All that matters is that we are at the lower left hand point.
If we now increase \(t\) (from whatever “starting” value we had) we know that cosine will need to increase from \(\cos \left( {\frac{5}{2}t} \right) = - 1\) until it reaches a value of \(\cos \left( {\frac{5}{2}t} \right) = 1\). By looking at the parametric equations we can see that this will also force both \(x\) and \(y\) to increase until it reaches the upper right-hand point.
Now, the graph won’t just stop here. Once cosine reaches a value of \(\cos \left( {\frac{5}{2}t} \right) = 1\) we know that continuing to increase \(t\) will now cause cosine to decrease it reaches a value of \(\cos \left( {\frac{5}{2}t} \right) = - 1\). This in turn forces both \(x\) and \(y\) to decrease until it once again reaches the lower left-hand point.
In other words, if we don’t put any restrictions on \(t\) a particle on this parametric curve will simply oscillate left and right along the portion of the square root sketched out above. In this case however we do have a range of \(t\)’s so we’ll need to determine a range of \(t\)’s for one trace to fully know the direction of motion information of the particle on this path and we’ll do that in the next step. With a restriction on the range of \(t\)’s it is possible that the particle won’t make a full trace or it might retrace some or all of the curve so we can’t say anything definite about the direction of motion for the particle over the full range of \(t\)’s until the next step when we determine a range of \(t\)’s for one full trace of the curve.
Show Step 4Now we need to determine a range of \(t\)’s for one full trace of the parametric curve. It is important for this step to remember that one full trace of the parametric curve means that no portion of the parametric curve can be retraced.
Note that one full trace does not mean that we get back to the “starting” point. When we dealt with an ellipse in a previous problem that was one trace because we did not need to retrace any portion of the ellipse to get back to the starting point. However, as we saw in the previous step that for our square root here we would have to retrace the full curve to get back to the starting point.
So, one full trace of the parametric curve means we move from the right end point to the left end point only or visa-versa and move from the left end point to the right end point. Which direction we move doesn’t really matter here so let’s get a range of \(t\)’s that take us from the left end point to the right end point.
In order to be at the left end point we need to require that \(\cos \left( {\frac{5}{2}t} \right) = - 1\) which occurs if \(\frac{5}{2}t = \ldots , - 3\pi , - \pi ,\pi ,3\pi , \ldots \). Note as well that unlike the previous problems, which had both sine and cosine, this set of parametric equations has only cosine and so all we need to do here is look at this. Also, in order to be at the right end point we need to require that \(\cos \left( {\frac{5}{2}t} \right) = 1\) which occurs if \(\frac{5}{2}t = \ldots , - 4\pi , - 2\pi ,0,2\pi ,4\pi , \ldots \).
So, if we want to move from the left to right all we need to do is chose one from the list of \(t\)’s corresponding to the left end point and then first \(t\) that comes that from the list corresponding to the right end point and we’ll have a range of \(t\)’s for one trace. To move from the right to left we just go the opposite direction, i.e. chose a \(t\) from the right end point list and then take the first \(t\) after that from the left end point list.
So, for this problem, since we said we were going to move from left to right, we’ll use \(\frac{5}{2}t = \pi \), which corresponds to \(t = \frac{2}{5}\pi \), for the left end point. That in turn means that we’ll need to use \(\frac{5}{2}t = 2\pi \), which corresponds to \(t = \frac{4}{5}\pi \), for the right end point. That means the range of \(t\)’s for one trace is,
\[\frac{2}{5}\pi \le t \le \frac{4}{5}\pi \]This is only one possible answer here. Any range of \(t\)’s with a “net” range of \(\frac{4}{5}\pi - \left( {\frac{2}{5}\pi } \right) = \frac{2}{5}\pi \) \(t\)’s, with the endpoints of the \(t\) range corresponding to start/end points of the parametric curve, will work. So, for example, any of the following ranges of \(t\)’s would also work.
\[ - \frac{2}{5}\pi \le t \le 0\hspace{0.25in}\hspace{0.25in}0 \le t \le \frac{2}{5}\pi \hspace{0.25in}\hspace{0.25in}\frac{4}{5}\pi \le t \le \frac{6}{5}\pi \]The direction of motion for each may be different range of \(t\)’s of course. Some will trace out the curve moving from left to right while others will trace out the curve moving from right to left. Because the problem did not specify a particular direction any would work.
Note as well that the range \(\frac{2}{5}\pi \le t \le \frac{4}{5}\pi \) falls completely inside the given range of \(t\)’s specified in the problem and so we know that the particle will trace out the curve more than once over the full range of \(t\)’s. Determining just how many times it traces over the curve will be determined in the next step.
Show Step 5Now that we have a range of \(t\)’s for one full trace of the parametric curve we can determine the number of traces the particle makes.
This is a really easy step. We know the total time the particle was traveling and we know how long it takes for a single trace. Therefore,
\[{\mbox{Number Traces = }}\frac{{{\mbox{Total Time Traveled}}}}{{{\mbox{Time for One Trace}}}} = \frac{{2\pi - \left( { - 48\pi } \right)}}{{\frac{4}{5}\pi - \left( {\frac{2}{5}\pi } \right)}} = \frac{{50\pi }}{{\frac{2}{5}\pi }} = 125{\mbox{ traces}}\] Show Step 6Finally, here is a sketch of the parametric curve for this set of parametric equations.
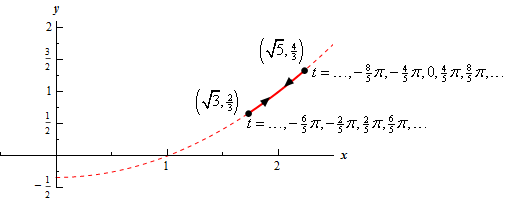
For this sketch we indicated the direction of motion by putting arrow heads going both directions in places on the curve. We also included a set of \(t\)’s for a couple of points to illustrate where the particle is at while tracing out of the curve as well as coordinates for the end points since they aren’t “nice” points.. The dashed line is the continuation of the square root from Step 1 to illustrate that our parametric curve is only a part of the square root.
Here is also the formal answers for all the rest of the information that problem asked for.
\[\begin{array}{lcc}{\mbox{Range of }}x{\mbox{ :}} & \hspace{0.1in} & \sqrt 3 \le x \le \sqrt 5 \\ {\mbox{Range of }}y{\mbox{ :}} & \hspace{0.1in} & \frac{2}{3} \le y \le \frac{4}{3}\\ {\mbox{Range of }}t{\mbox{ for one trace : }} & \hspace{0.1in} & \frac{2}{5}\pi \le t \le \frac{4}{5}\pi \\ {\mbox{Total number of traces : }} & \hspace{0.1in} & 125\end{array}\]