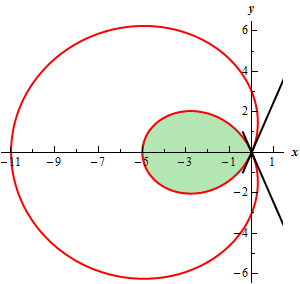
Now, we’ll need to determine the values of \(\theta \) that the graph goes through the origin (indicated by the black lines on the graph in the previous step).

There are easy enough to find. Because they are where the graph goes through the origin we know that we must have \(r = 0\). So,

\[\begin{align*}3 - 8\cos \theta & = 0\\ \cos \theta & = \frac{3}{8}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = {\cos ^{ - 1}}\left( {\frac{3}{8}} \right) = 1.1864\end{align*}\]

This is the angle in the first quadrant where the graph goes through the origin.

We next need the angle in the fourth quadrant. We need to be a little careful with this second angle. We need to always remember that the limits on the integral we’ll eventually be computing must go from smaller to larger value. Also, as the angle moves from the smaller to larger value they must trace out the boundary curve of the region we are interested in.

From a quick sketch of a unit circle we can quickly get two possible values for the angle in the fourth quadrant.

\[\theta = 2\pi - 1.1864 = 5.0968\hspace{0.75in}\theta = - 1.1864\]

Depending upon the problem we are being asked to do either of these could be the one we need. However, in this case we can see that if we use the first angle (i.e. the positive angle) we actually end up tracing out the outer portion of the curve and that isn’t what we want here. However, if we use the second angle (i.e. the negative angle) we will trace out the inner loop as we move from this angle to the angle in the first quadrant.

So, for this particular problem, we need to use \(\theta = - 1.1864\).

The ranges of \(\theta \) for this problem is then \( - 1.1864 \le \theta \le 1.1864\).

Show Step 3

The area of the inner loop is then,

\[\begin{align*}A & = \int_{{ - 1.1864}}^{{1.1864}}{{\frac{1}{2}{{\left( {3 - 8\cos \theta } \right)}^2}\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 1.1864}}^{{1.1864}}{{9 - 48\cos \theta + 64co{s^2}\left( \theta \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 1.1864}}^{{1.1864}}{{9 - 48\cos \theta + 32\left( {1 + \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \frac{1}{2}\int_{{ - 1.1864}}^{{1.1864}}{{41 - 48\cos \theta + 32\cos \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( {41\theta - 48\sin \left( \theta \right) + 16\sin \left( {2\theta } \right)} \right)} \right|_{ - 1.1864}^{1.1864} = \require{bbox} \bbox[2pt,border:1px solid black]{{15.2695}}\end{align*}\]

Make sure you can do the trig manipulations required to do these integrals. Most of the integrals in this section will involve this kind of manipulation. If you don’t recall how to do them go back and take a look at the Integrals Involving Trig Functions section.