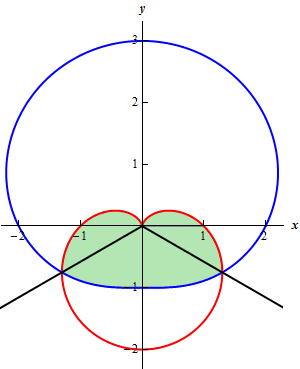
Now, we’ll need to determine the values of \(\theta \) where the graphs intersect (indicated by the black lines on the graph in the previous step).

There are easy enough to find. Because they are where the graphs intersect we know they must have the same value of \(r\). So,

\[\begin{align*}2 + \sin \theta & = 1 - \sin \theta \\ \sin\theta & = - \frac{1}{2}\hspace{0.5in} \Rightarrow \hspace{0.5in}\theta = {\sin ^{ - 1}}\left( { - \frac{1}{2}} \right) = - \frac{\pi }{6}\end{align*}\]

This is one possible value for the angle in the fourth quadrant where the graphs intersect. From a quick sketch of a unit circle we can see that a second possible value for this angle is,

\[\theta = 2\pi - \frac{\pi }{6} = \frac{{11\pi }}{6}\]

From a quick sketch of a unit circle we can quickly get a value for the angle in the third quadrant where the two graphs intersect.

\[\theta = \pi + \frac{\pi }{6} = \frac{{7\pi }}{6}\]

Okay. We now have a real problem. Recall that the angles must go from smaller to larger values and as they do that they must trace out the boundary curves of the enclosed area.

If we use \( - \frac{\pi }{6} \le \theta \le \frac{{7\pi }}{6}\) we actually end up tracing out the large “open” or unshaded region that lies above the shaded region.

Likewise, if we use \(\frac{{7\pi }}{6} \le \theta \le \frac{{11\pi }}{6}\) we actually end up tracing out the smaller “open” or unshaded region that lies below the shaded region.

In other words, we can’t find the shaded area simply by using the formula from this section.

Show Step 3

As we saw in the previous step we can’t just compute an integral in order to get the area of the shaded region. However, that doesn’t mean that we can’t find the area of the shaded region. We just need to work a little harder at it for this problem.

To find the area of the shaded area we can notice that the shaded area is really nothing more than the remainder of the area inside \(r = 2 + \sin \theta \) once we take out the portion that is also outside \(r = 1 - \sin \theta \).

Another way to look at is that the shaded area is simply the remainder of the area inside \(r = 1 - \sin \theta \) once we take out the portion that is also outside \(r = 2 + \sin \theta \).

We can use either of these ideas to find the area of the shaded region. We’ll use the first one for no other reason that it was the first one listed.

If we knew the total area that is inside \(r = 2 + \sin \theta \) (which we can find with a simple integral) and if we also knew the area that is inside \(r = 2 + \sin \theta \) and outside \(r = 1 - \sin \theta \) then the shaded area is nothing more than the difference between these two areas.

Show Step 4

Okay, let’s start this off by getting the total area that is inside \(r = 2 + \sin \theta \). This can be found by evaluating the following integral.

\[\begin{align*}A & = \int_{0}^{{2\pi }}{{\frac{1}{2}{{\left( {2 + \sin \theta } \right)}^2}\,d\theta }}\\ & = \frac{1}{2}\int_{0}^{{2\pi }}{{4 + 4\sin \theta + {{\sin }^2}\left( \theta \right)\,d\theta }}\\ & = \frac{1}{2}\int_{0}^{{2\pi }}{{4 + 4\sin \theta + \frac{1}{2}\left( {1 - \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \frac{1}{2}\int_{0}^{{2\pi }}{{\frac{9}{2} + 4\sin \theta - \frac{1}{2}\cos \left( {2\theta } \right)\,d\theta }}\\ & = \left. {\frac{1}{2}\left( {\frac{9}{2}\theta - 4\cos \left( \theta \right) - \frac{1}{4}\sin \left( {2\theta } \right)} \right)} \right|_0^{2\pi } = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{9\pi }}{2}}}\end{align*}\]

Note that we need to do a full “revolution” to get all the area inside \(r = 2 + \sin \theta \) and so we used the range \(0 \le \theta \le 2\pi \) for this integral.

Show Step 5

Now, the area that is inside \(r = 2 + \sin \theta \) and outside \(r = 1 - \sin \theta \) is,

\[\begin{align*}A & = \int_{{ - \,\frac{\pi }{6}}}^{{\frac{{7\pi }}{6}}}{{\frac{1}{2}\left[ {{{\left( {2 + \sin \theta } \right)}^2} - {{\left( {1 - \sin \theta } \right)}^2}} \right]\,d\theta }}\\ & = \frac{1}{2}\int_{{ - \,\frac{\pi }{6}}}^{{\frac{{7\pi }}{6}}}{{3 + 6\sin \theta \,d\theta }}\\ & = \frac{1}{2}\left. {\left( {3\theta - 6\cos \left( \theta \right)} \right)} \right|_{ - \,\frac{\pi }{6}}^{\frac{{7\pi }}{6}} = \require{bbox} \bbox[2pt,border:1px solid black]{{2\pi + 3\sqrt 3 }}\end{align*}\]

Note that we found the limits for this region in Step 2.

Show Step 6

Finally, the shaded area is simply,

\[A = \frac{{9\pi }}{2} - \left( {2\pi + 3\sqrt 3 } \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{5}{2}\pi - 3\sqrt 3 = 2.6578}}\]