Section 9.6 : Polar Coordinates
14. Sketch the graph of the following polar equation.
\[r = 8 + 8\cos \theta \] Show SolutionWe know from the notes on this section that this is a cardioid and so all we really need to get the graph is a quick chart of points.
| \(\theta \) | \(r\) | \(\left( {r,\theta } \right)\) |
|---|---|---|
| 0 | 16 | \(\left( {16,0} \right)\) |
| \(\displaystyle \frac{\pi }{2}\) | 8 | \(\left( {8,\displaystyle \frac{\pi }{2}} \right)\) |
| \(\pi \) | 0 | \(\left( {0,\pi } \right)\) |
| \(\displaystyle \frac{{3\pi }}{2}\) | 8 | \(\left( {8,\displaystyle \frac{{3\pi }}{2}} \right)\) |
| \(2\pi \) | 16 | \(\left( {16,2\pi } \right)\) |
So here is the graph of this function.
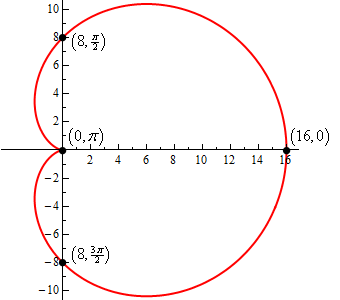
Be careful when plotting these points and remember the rules for graphing polar coordinates. The “tick marks” on the graph are really the Cartesian coordinate tick marks because those are the ones we are familiar with. Do not let them confuse you when you go to plot the polar points for our sketch.