I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 9.6 : Polar Coordinates
15. Sketch the graph of the following polar equation.
\[r = 5 - 2\sin \theta \] Show SolutionWe know from the notes on this section that this is a limacon without an inner loop and so all we really need to get the graph is a quick chart of points.
| \(\theta \) | \(r\) | \(\left( {r,\theta } \right)\) |
|---|---|---|
| 0 | 5 | \(\left( {5,0} \right)\) |
| \(\displaystyle \frac{\pi }{2}\) | 3 | \(\left( {3,\displaystyle \frac{\pi }{2}} \right)\) |
| \(\pi \) | 5 | \(\left( {5,\pi } \right)\) |
| \(\displaystyle \frac{{3\pi }}{2}\) | 7 | \(\left( {7,\displaystyle \frac{{3\pi }}{2}} \right)\) |
| \(2\pi \) | 5 | \(\left( {5,2\pi } \right)\) |
So here is the graph of this function.
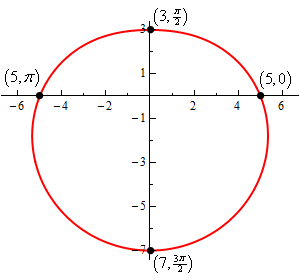
Be careful when plotting these points and remember the rules for graphing polar coordinates. The “tick marks” on the graph are really the Cartesian coordinate tick marks because those are the ones we are familiar with. Do not let them confuse you when you go to plot the polar points for our sketch.
Also, many of these graphs are vaguely heart shaped although as this sketch has shown many do and this one is more circular than heart shaped.