Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 12.4 : Quadric Surfaces
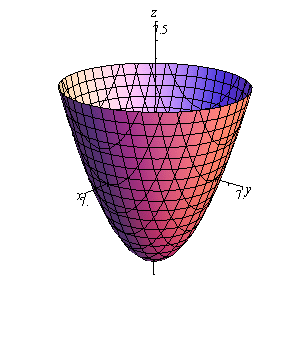
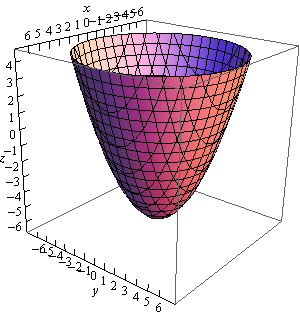
3. Sketch the following quadric surface.
\[z = \frac{{{x^2}}}{4} + \frac{{{y^2}}}{4} - 6\] Show SolutionThis is an elliptic paraboloid that is centered on the \(z\)-axis. Because the \(x\) and \(y\) terms are positive we know that it will open upwards. The “-6” tells us that the surface will start at \(z = - 6\). We can also say that because the coefficients of the \(x\) and \(y\) terms are identical the cross sections of the surface will be circles.
Here are a couple of sketches of the region. We’ve given them with the more traditional axes as well as “boxed” axes to help visualize the surface.