Section 15.1 : Double Integrals
1. Use the Midpoint Rule to estimate the volume under \(f\left( {x,y} \right) = {x^2} + y\) and above the rectangle given by \( - 1 \le x \le 3\), \(0 \le y \le 4\) in the \(xy\)-plane. Use 4 subdivisions in the \(x\) direction and 2 subdivisions in the \(y\) direction.
Show All Steps Hide All Steps
Start SolutionOkay, first let’s get a quick sketch of the rectangle we’re dealing with here.
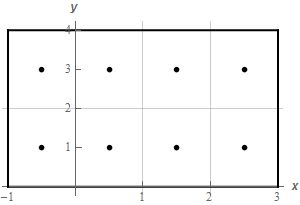
The light gray lines show the subdivisions for each direction. The dots in the center of each “block” are the midpoints of each of the blocks.
The coordinates of each of the dots in the lower row are,
\[\left( { - \frac{1}{2},1} \right)\hspace{0.25in}\left( {\frac{1}{2},1} \right)\hspace{0.25in}\left( {\frac{3}{2},1} \right)\hspace{0.25in}\left( {\frac{5}{2},1} \right)\]and the coordinates of each of the dots in the upper row are,
\[\left( { - \frac{1}{2},3} \right)\hspace{0.25in}\left( {\frac{1}{2},3} \right)\hspace{0.25in}\left( {\frac{3}{2},3} \right)\hspace{0.25in}\left( {\frac{5}{2},3} \right)\] Show Step 2We know that the volume we are after is simply,
\[V = \iint\limits_{R}{{f\left( {x,y} \right)\,dA}}\]and we also know that the Midpoint Rule for this particular case is the following double summation.
\[\iint\limits_{R}{{f\left( {x,y} \right)\,dA}} \approx \sum\limits_{i = 1}^4 {\sum\limits_{j = 1}^2 {f\left( {{{\overline{x}}_i},{{\overline{y}}_j}} \right)\,\Delta {\kern 1pt} A} } \hspace{0.25in}\hspace{0.25in}f\left( {x,y} \right) = {x^2} + y\]Remember that there are four \(x\) subdivisions and so the \(i\) summation will go to 4. There are two \(y\) subdivisions and the \(j\) summation will go to 2.
The \(\left( {{{\overline{x}}_i},{{\overline{y}}_j}} \right)\) in the formula are simply the midpoints of each of the blocks (i.e. the points listed in Step 1 above) and \(\Delta {\kern 1pt} A\) is the area of each of blocks and so is \(\Delta {\kern 1pt} A = \left( 1 \right)\left( 2 \right) = 2\).
Therefore, the volume for this problem is approximately,
\[V \approx \sum\limits_{i = 1}^4 {\sum\limits_{j = 1}^2 {2f\left( {{{\overline{x}}_i},{{\overline{y}}_j}} \right)\,} } \hspace{0.25in}\hspace{0.25in}f\left( {x,y} \right) = {x^2} + y\]Note that we plugged \(\Delta {\kern 1pt} A\) into the formula.
Show Step 3The best way to compute this double summation is probably to first compute the “inner” summation for each value of \(i\).
Each of the inner summations are done for a fixed value of \(i\) as \(i\) runs from \(i = 1\) to \(i = 4\). Therefore, the four inner summations are computed using the values of the function at the midpoints for the blocks in each of the columns in the sketch above in Step 1.
This means we need the following summations.
\[\begin{align*}& i = 1\,\,\,\,:\,\,\,\,\,\sum\limits_{j = 1}^2 {2f\left( {{{\overline{x}}_1},{{\overline{y}}_j}} \right)\, = } \sum\limits_{j = 1}^2 {2f\left( { - \frac{1}{2},{{\overline{y}}_j}} \right)\,} = 2\left[ {f\left( { - \frac{1}{2},1} \right) + f\left( { - \frac{1}{2},3} \right)} \right] = 9\\ & i = 2\,\,\,\,:\,\,\,\,\,\sum\limits_{j = 1}^2 {2f\left( {{{\overline{x}}_2},{{\overline{y}}_j}} \right)\,} = \sum\limits_{j = 1}^2 {2f\left( {\frac{1}{2},{{\overline{y}}_j}} \right)\,} = 2\left[ {f\left( {\frac{1}{2},1} \right) + f\left( {\frac{1}{2},3} \right)} \right] = 9\\ & i = 3\,\,\,\,:\,\,\,\,\,\sum\limits_{j = 1}^2 {2f\left( {{{\overline{x}}_3},{{\overline{y}}_j}} \right) = \,} \sum\limits_{j = 1}^2 {2f\left( {\frac{3}{2},{{\overline{y}}_j}} \right)\,} = 2\left[ {f\left( {\frac{3}{2},1} \right) + f\left( {\frac{3}{2},3} \right)} \right] = 17\\ & i = 4\,\,\,\,:\,\,\,\,\,\sum\limits_{j = 1}^2 {2f\left( {{{\overline{x}}_4},{{\overline{y}}_j}} \right) = \,} \sum\limits_{j = 1}^2 {2f\left( {\frac{5}{2},{{\overline{y}}_j}} \right)\,} = 2\left[ {f\left( {\frac{5}{2},1} \right) + f\left( {\frac{5}{2},3} \right)} \right] = 33\end{align*}\] Show Step 4We can now compute the “outer” summation. This is just the sum of all the inner summations we computed in Step 3.
The volume is then approximately,
\[V \approx \sum\limits_{i = 1}^4 {\sum\limits_{j = 1}^2 {2f\left( {{{\overline{x}}_i},{{\overline{y}}_j}} \right)\,} } = 9 + 9 + 17 + 33 = \require{bbox} \bbox[2pt,border:1px solid black]{{68}}\]For reference purposes we will eventually be able to verify that the exact volume is \(\frac{{208}}{3} = 69.333\overline 3 \) and so the approximation in this case is actually fairly close.