Section 16.7 : Green's Theorem
1. Use Green’s Theorem to evaluate \( \displaystyle \int\limits_{C}{{y{x^2}\,dx - {x^2}\,dy}}\) where \(C\) is shown below.
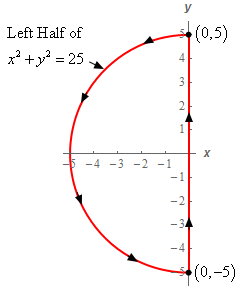
Show All Steps Hide All Steps
Start SolutionOkay, first let’s notice that if we walk along the path in the direction indicated then our left hand will be over the enclosed area and so this path does have the positive orientation and we can use Green’s Theorem to evaluate the integral.
From the integral we have,
\[P = y{x^2}\hspace{0.25in}\hspace{0.25in}Q = - {x^2}\]Remember that \(P\) is multiplied by \(x\) and \(Q\) is multiplied by \(y\) and don’t forget to pay attention to signs. It is easy to get in a hurry and miss a sign in front of one of the terms.
Show Step 2Using Green’s Theorem the line integral becomes,
\[\int\limits_{C}{{y{x^2}\,dx - {x^2}\,dy}} = \iint\limits_{D}{{ - 2x - {x^2}\,dA}}\]\(D\) is the region enclosed by the curve.
Show Step 3Since \(D\) is just a half circle it makes sense to use polar coordinates for this problem. The limits for \(D\) in polar coordinates are,
\[\begin{array}{c}\displaystyle \frac{1}{2}\pi \le \theta \le \frac{3}{2}\pi \\ 0 \le r \le 5\end{array}\] Show Step 4Now all we need to do is evaluate the double integral, after first converting to polar coordinates of course.
Here is the evaluation work.
\[\begin{align*}\int\limits_{C}{{y{x^2}\,dx - {x^2}\,dy}} & = \iint\limits_{D}{{ - 2x - {x^2}\,dA}}\\ & = \int_{{\frac{1}{2}\pi }}^{{\frac{3}{2}\pi }}{{\int_{0}^{5}{{r\left( { - 2r\cos \theta - {r^2}{{\cos }^2}\theta } \right)dr}}\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{{\frac{3}{2}\pi }}{{\int_{0}^{5}{{ - 2{r^2}\cos \theta - \frac{1}{2}{r^3}\left( {1 + \cos \left( {2\theta } \right)} \right)dr}}\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{{\frac{3}{2}\pi }}{{\left. {\left( { - \frac{2}{3}{r^3}\cos \theta - \frac{1}{8}{r^4}\left( {1 + \cos \left( {2\theta } \right)} \right)} \right)} \right|_0^5\,d\theta }}\\ & = \int_{{\frac{1}{2}\pi }}^{{\frac{3}{2}\pi }}{{ - \frac{{250}}{3}\cos \theta - \frac{{625}}{8}\left( {1 + \cos \left( {2\theta } \right)} \right)\,d\theta }}\\ & = \left. {\left[ { - \frac{{250}}{3}\sin \theta - \frac{{625}}{8}\left( {\theta + \frac{1}{2}\sin \left( {2\theta } \right)} \right)} \right]} \right|_{\frac{1}{2}\pi }^{\frac{3}{2}\pi }\\ & = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{500}}{3} - \frac{{625}}{8}\pi = - 78.7703}}\end{align*}\]Don’t forget the extra \(r\) from converting the \(A\) to polar coordinates and make sure you recall all the various tirg identities we need to deal with many of the various trig functions that show up in the integrals.