Calculus III - Green's Theorem

Show Mobile Notice Show All Notes Hide All Notes

Mobile Notice

You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width.

Section 16.7 : Green's Theorem

Back to Problem List

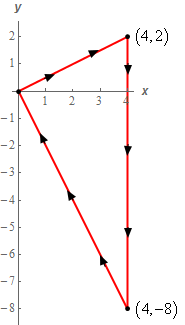
3. Use Green’s Theorem to evaluate \( \displaystyle \int\limits_{C}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}}\) where \(C\) is shown below.

Show All Steps Hide All Steps

Start Solution

Okay, first let’s notice that if we walk along the path in the direction indicated then our left hand will NOT be over the enclosed area and so this path does NOT have the positive orientation. This, in turn, means that we can’t actually use Green’s Theorem to evaluate the given integral.

However, if \(C\) has the negative orientation then –\(C\) will have the positive orientation and we know how to relate the values of the line integrals over these two curves. Specifically, we know that,

\[\int\limits_{C}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}} = - \int\limits_{{ - C}}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}}\]

So, instead of using Green’s Theorem to compute the value of the integral in the problem statement we’ll use Green’s Theorem to compute the value of the following integral.

\[\int\limits_{{ - C}}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}}\]

From this integral we have,

\[P = {x^2}{y^2}\hspace{0.25in}\hspace{0.25in}Q = y{x^3} + {y^2}\]

Remember that \(P\) is multiplied by \(x\) and \(Q\) is multiplied by \(y\).

Show Step 2

Using Green’s Theorem the line integral from over \( - C\) becomes,

\[\int\limits_{{ - C}}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}} = \iint\limits_{D}{{3y{x^2} - 2y{x^2}\,dA}} = \iint\limits_{D}{{y{x^2}\,dA}}\]

\(D\) is the region enclosed by the curve.

Show Step 3

We’ll leave it to you to verify that the equation of the line along the top of the region is given by \(y = \frac{1}{2}x\) and the equation of the line along the bottom of the region is given by \(y = - 2x\). Once we have these equations the region is then very easy to get limits for. They are,

\[\begin{array}{c}0 \le x \le 4\\ \displaystyle - 2x \le y \le \frac{1}{2}x\end{array}\] Show Step 4

Now all we need to do is evaluate the double integral to get the value of the line integral from \( - C\). Here is the evaluation work.

\[\begin{align*}\int\limits_{{ - C}}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}} & = \iint\limits_{D}{{y{x^2}\,dA}}\\ & = \int_{0}^{4}{{\int_{{ - 2x}}^{{\frac{1}{2}x}}{{y{x^2}\,dy}}\,dx}}\\ & = \int_{0}^{4}{{\left. {\frac{1}{2}{y^2}{x^2}} \right|_{ - 2x}^{\frac{1}{2}x}\,dx}}\\ & = \int_{0}^{4}{{ - \frac{{15}}{8}{x^4}\,dx}}\\ & = \left. { - \frac{{3{x^5}}}{8}} \right|_0^4 = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 384}}\end{align*}\]

Show Step 5

Okay, now we can’t forget that the integral in Step 4 was not the integral we were asked to find the value of. Using the relationship between the value of the integrals over \(C\) and –\(C\) we know that the value of the integral we were asked to compute is,

\[\int\limits_{C}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}} = - \int\limits_{{ - C}}{{{x^2}{y^2}\,dx + \left( {y{x^3} + {y^2}} \right)\,dy}} = \require{bbox} \bbox[2pt,border:1px solid black]{{384}}\]