Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 12.5 : Functions of Several Variables
4. Find the domain of the following function.
\[f\left( {x,y} \right) = \frac{1}{x} + \sqrt {y + 4} - \sqrt {x + 1} \] Show SolutionThere really isn’t all that much to this problem. We know that we can’t have division by zero and we can’t take square roots of negative numbers and so we’ll need to require that whatever \(\left( {x,y} \right)\) is it will need to satisfy the following three conditions.
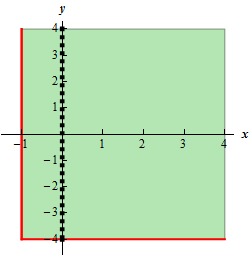
\[x \ge - 1\hspace{0.5in}x \ne 0\hspace{0.5in}y \ge - 4\]This is also our domain since these are the only conditions require in order for the function to exist.
A sketch of the domain is shown below. We can take any point in the green area or on the red lines with the exception of the \(y\)-axis (i.e. \(x \ne 0\)) as indicated by the black dashes on the \(y\)-axis.