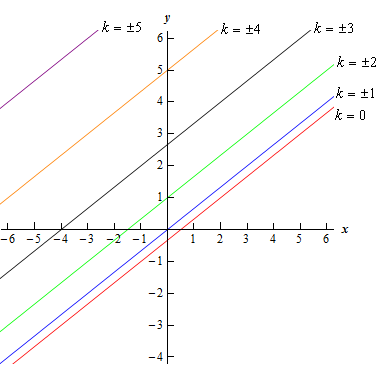Section 12.5 : Functions of Several Variables
5. Identify and sketch the level curves (or contours) for the following function.
\[2x - 3y + {z^2} = 1\]Show All Steps Hide All Steps
Start SolutionWe know that level curves or contours are given by setting \(z = k\). Doing this in our equation gives,
\[2x - 3y + {k^2} = 1\] Show Step 2A quick rewrite of the equation from the previous step gives us,
\[y = \frac{2}{3}x + \frac{{{k^2} - 1}}{3}\]So, the level curves for this function will be lines with slope \(\frac{2}{3}\) and a \(y\)-intercept of \(\left( {0,\frac{{{k^{\,2}} - 1}}{3}} \right)\).
Note as well that there will be no restrictions on the values of \(k\) that we can use, as there sometimes are. Also note that the sign of \(k\) will not matter so, with the exception of the level curve for \(k = 0\), each level curve will in fact arise from two different values of \(k\).
Show Step 3Below is a sketch of some level curves for some values of \(k\) for this function.