Section 12.5 : Functions of Several Variables
9. Identify and sketch the traces for the following function.
\[4z + 2{y^2} - x = 0\]Show All Steps Hide All Steps
Start SolutionWe have two traces. One we get by plugging \(x = a\) into the equation and the other we get by plugging \(y = b\) into the equation. Here is what we get for each of these.
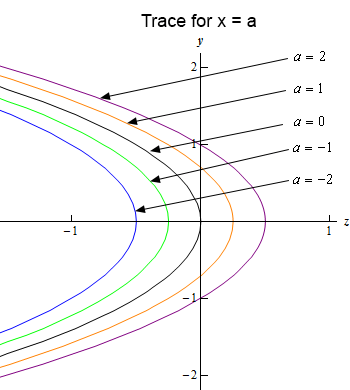
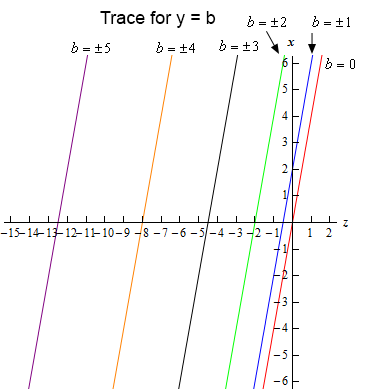
\[\begin{align*}x = a: & \hspace{0.25in}4z + 2{y^2} - a = 0 & \to \hspace{0.25in} & z = - \frac{1}{2}{y^2} + \frac{a}{4}\\ y = b: & \hspace{0.25in}4z + 2{b^2} - x = 0 & \to \hspace{0.25in} & x = 4z + 2{b^2}\end{align*}\] Show Step 2Okay, we’re now into a realm that many students have issues with initially. We no longer have equations in terms of \(x\) and \(y\). Instead we have one equation in terms of \(x\) and \(z\) and another in terms of \(y\) and \(z\).
Do not get excited about this! They work the same way that equations in terms of \(x\) and \(y\) work! The only difference is that we need to make a decision on which variable will be the horizontal axis variable and which variable will be the vertical axis variable.
Just because we have an \(x\) doesn’t mean that it must be the horizontal axis and just because we have a \(y\) doesn’t mean that it must be the vertical axis! We set up the axis variables in a way that will be convenient for us.
In this case since both equation have a \(z\) in them we’ll let \(z\) be the horizontal axis variable for both of the equations.
So, given that convention for the axis variables this means that for the \(x = a\) trace we’ll have a parabola that opens to the left with vertex at \(\left( {\frac{a}{4},0} \right)\) and for the \(y = b\) trace we’ll have a line with slope of 4 and an \(x\)-intercept at \(\left( {0,2{b^2}} \right)\).
Show Step 3Below is a sketch for each of the traces.