Now, the set of parametric equations from above is for the full plane and that isn’t what we want in this problem. In this problem we only want the portion of the plane that is in the 1^st octant.

So, we’ll need to restrict \(x\) and \(y\) so that the parametric equation from Step 1 will only give the portion of the plane that is in the 1^st octant.

If you recall how to get the region \(D\) for a triple integral then you know how to do this because it is basically the same idea. In this case we need the region \(D\) in the \(xy\)-plane that will give the plane in the 1^st octant.

Here is a sketch of this region.

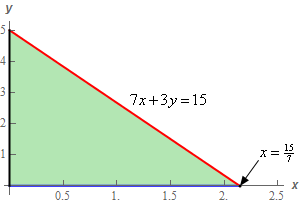
The hypotenuse is just where the plane intersects the \(xy\)-plane and so we can quickly find the equation of the line by setting \(z = 0\) in the equation of the plane.

We can either solve this for \(x\) or \(y\) to get the ranges for \(x\) and \(y\). It doesn’t really matter which we solve for here so let’s just solve for \(y\) to get the following ranges for \(x\) and \(y\) to describe this triangle.

\[\begin{array}{c} \displaystyle 0 \le x \le \frac{{15}}{7}\\ \displaystyle 0 \le y \le - \frac{7}{3}x + 5\end{array}\]

Putting this all together we get the following set of parametric equations for the plane that is in the 1^st octant.

\[\require{bbox} \bbox[2pt,border:1px solid black]{{\vec r\left( {x,y} \right) = \left\langle {x,y,\frac{{15}}{4} - \frac{7}{4}x - \frac{3}{4}y} \right\rangle \,\,\,\,\,\,\,\,\,0 \le x \le \frac{{15}}{7}\,\,\,,\,\,0 \le y \le - \frac{7}{3}x + 5}}\]