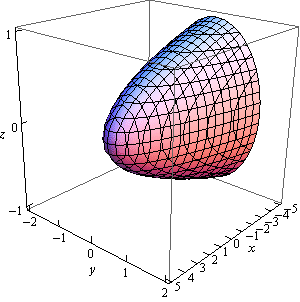Section 12.4 : Quadric Surfaces
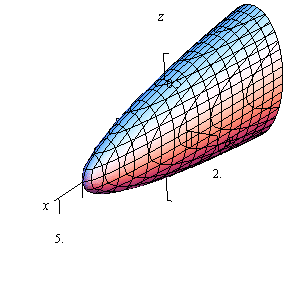
5. Sketch the following quadric surface.
\[x = 4 - 5{y^2} - 9{z^2}\] Show SolutionThis is an elliptic paraboloid that is centered on the \(x\)-axis. Because the \(y\) and \(z\) terms are negative we know that it will open in the negative \(x\) direction. The “4” tells us that the surface will start at \(x = 4\). We can also say that because the coefficients of the \(y\) and \(z\) terms are different the cross sections of the surface will be ellipses.
Make sure that you can “translate” the equations given in the notes to the other coordinate axes. Once you know what they look like when centered on one of the coordinates axes then a simple and predictable variable change will center them on the other coordinate axes.
Here are a couple of sketches of the region. We’ve given them with the more traditional axes as well as “boxed” axes to help visualize the surface.