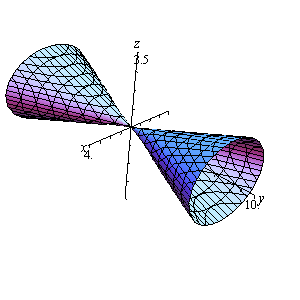Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 12.4 : Quadric Surfaces
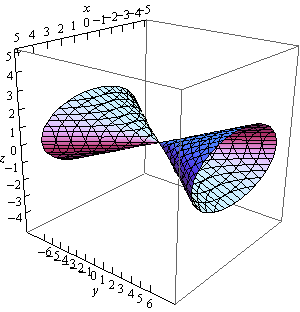
4. Sketch the following quadric surface.
\[{y^2} = 4{x^2} + 16{z^2}\] Show SolutionThis is a cone that is centered on the \(y\)-axis and because the coefficients of the \(x\) and \(z\) terms are different the cross sections of the surface will be ellipses.
Make sure that you can “translate” the equations given in the notes to the other coordinate axes. Once you know what they look like when centered on one of the coordinates axes then a simple and predictable variable change will center them on the other coordinate axes.
Here are a couple of sketches of the region. We’ve given them with the more traditional axes as well as “boxed” axes to help visualize the surface.