Section 15.9 : Surface Area
3. Determine the surface area of the portion of \(\displaystyle z = 3 + 2y + \frac{1}{4}{x^4}\) that is above the region in the \(xy\)-plane bounded by \(y = {x^5}\), \(x = 1\) and the \(x\)-axis.
Show All Steps Hide All Steps
Start SolutionOkay, let’s start off with a quick sketch of the surface so we can get a feel for what we’re dealing with.
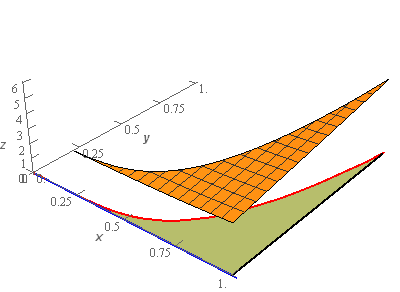
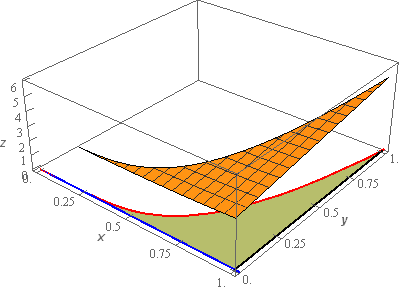
We’ve given the sketches with a set of “traditional” axes as well as a set of “box” axes to help visualize the surface.
The surface we are after is the orange portion that is above the \(xy\)-plane and the greenish region in the \(xy\)-plane is the region over which we are graphing the surface, i.e. it is the region \(D\) we’ll use in the integral.
Show Step 2The integral for the surface area is,
\[S = \iint\limits_{D}{{\sqrt {{{\left[ {{x^3}} \right]}^2} + {{\left[ 2 \right]}^2} + 1} \,dA}} = \iint\limits_{D}{{\sqrt {{x^6} + 5} \,dA}}\] Show Step 3Now, as mentioned in Step 1 the region \(D\) is shown in the sketches of the surface. Here is a 2D sketch of \(D\) for the sake of completeness.
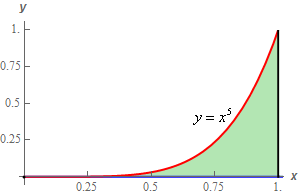
The limits for this region are,
\[\begin{array}{c}0 \le x \le 1\\ 0 \le y \le {x^5}\end{array}\]Note as well that the integrand pretty much requires us to do the integration in this order.
Show Step 4With the limits from Step 3 the integral becomes,
\[S = \iint\limits_{D}{{\sqrt {{x^6} + 5} \,dA}} = \int_{0}^{1}{{\int_{0}^{{{x^5}}}{{\sqrt {{x^6} + 5} \,dy}}\,dx}}\] Show Step 5Okay, all we need to do then is evaluate the integral.
\[\begin{align*}S & = \int_{0}^{1}{{\int_{0}^{{{x^5}}}{{\sqrt {{x^6} + 5} \,dy}}\,dx}}\\ & = \int_{0}^{1}{{\left. {\left( {y\sqrt {{x^6} + 5} } \right)} \right|_0^{{x^5}}\,dx}}\\ & = \int_{0}^{1}{{{x^5}\sqrt {{x^6} + 5} \,dx}}\\ & = \left. {\frac{1}{9}{{\left( {{x^6} + 5} \right)}^{\frac{3}{2}}}} \right|_0^1 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{9}\left( {{6^{\frac{3}{2}}} - {5^{\frac{3}{2}}}} \right) = 0.3907}}\end{align*}\]