Section 15.9 : Surface Area
5. Determine the surface area region formed by the intersection of the two cylinders \({x^2} + {y^2} = 4\) and \({x^2} + {z^2} = 4\).
Show All Steps Hide All Steps
Start SolutionWe looked at the volume of this region back in the Double Integral practice problem section. Now we are going to look at the surface area of this region.
Visualizing the surface/region we’re looking at is probably one of the harder parts of this problem. So, let’s start off with a sketch of the two cylinders.

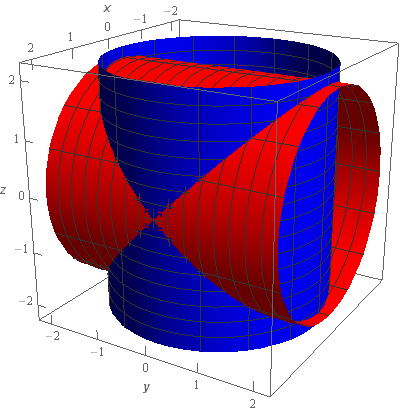
The blue cylinder is the cylinder centered on the \(z\)-axis (i.e. \({x^2} + {y^2} = 4\)) and the red cylinder is the cylinder centered on the \(y\)-axis (i.e. \({x^2} + {z^2} = 4\)).
Now, the surface/region we need is the intersection of these two cylinders. So, taking away the “extra” bits of the cylinders that are outside of the intersection we get the following sketches.

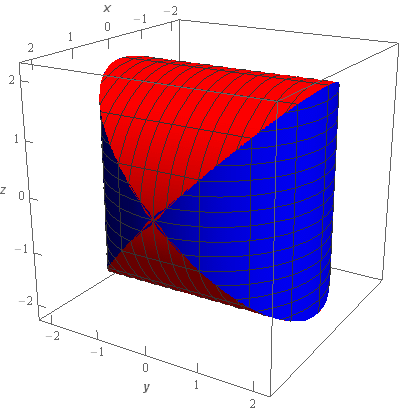
The blue part of this sketch is the portion of \({x^2} + {y^2} = 4\) that is inside of \({x^2} + {z^2} = 4\) and the red part of this sketch is the portion of \({x^2} + {z^2} = 4\) that is inside of \({x^2} + {y^2} = 4\). Taken together we get the surface/region we are interested in.
Now, when we did the volume of this region the sketches above were sufficient for our purposes. This time let’s do one more set of sketches.

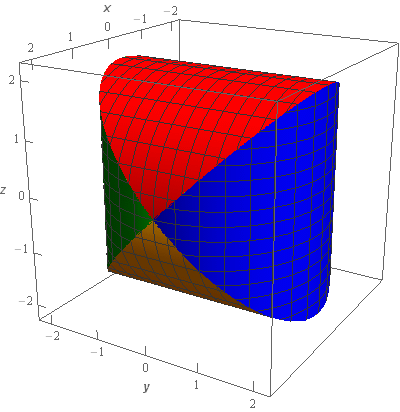
In this sketch the blue and green parts of the sketch are the right and left portions of \({x^2} + {y^2} = 4\) respectively and the red and yellow parts of the sketch are the upper and lower portion of \({x^2} + {z^2} = 4\) respectively.
Show Step 2Now, we need to set up an integral that will give the surface area of this surface/region.
Let’s first notice that by symmetry the red and yellow surfaces must have the same surface area since they are simply the upper/lower portion of the same cylinder. Likewise the blue and green surfaces will have the same surface area.
Next, because both of the cylinders that make up this surface have the same radius the upper/lower and right/left portions also must have the same surface area.
So, this means that all we need to do is get the surface area of one of the four surfaces shown above and we can them get the full surface area by multiplying that number by four.
So, let’s get the surface area of the red portion of the sketch above. To do this we’ll need to solve \({x^2} + {z^2} = 4\) for \(z\) to get,
\[z = \pm \sqrt {4 - {x^2}} \]The “+” equation will give the red portion of the sketch and the “-” equation will give the yellow portion of the sketch.
So, let’s set up the integral that will give the surface area of the red portion. The integral is,
\[\begin{align*}S & = \iint\limits_{D}{{\sqrt {{{\left[ {{f_x}} \right]}^2} + {{\left[ {{f_y}} \right]}^2} + 1} \,dA}} = \iint\limits_{D}{{\sqrt {{{\left[ {\frac{{ - x}}{{\sqrt {4 - {x^2}} }}} \right]}^2} + {{\left[ 0 \right]}^2} + 1} \,dA}}\\ & = \iint\limits_{D}{{\sqrt {\frac{{{x^2}}}{{4 - {x^2}}} + 1} \,dA}} = \iint\limits_{D}{{\sqrt {\frac{{{x^2} + \left( {4 - {x^2}} \right)}}{{4 - {x^2}}}} \,dA}} = \iint\limits_{D}{{\sqrt {\frac{4}{{4 - {x^2}}}} \,dA}}\\ & = \iint\limits_{D}{{\frac{2}{{\sqrt {4 - {x^2}} }}\,dA}}\end{align*}\]Do not get excited about the fact that one of the derivatives in the formula ended up being zero. This will happen on occasion so we don’t want to get excited about it when it happens.
Note as well that we did a fair amount of simplification. Notably, after taking the \(x\) derivative and squaring we set up the terms under the radical to have the same dominator. This in turn gave us a single rational expression under the radical that we could easily take the root of both the numerator and denominator.
As we will eventually see all this simplification will make the integral evaluation work a lot simpler.
Show Step 3Now, we need to determine the region \(D\) for our integral. If we looked at the surface from directly above (i.e. down along the \(z\)-axis) we see the following figure.

The blue circle is in fact the cylinder \({x^2} + {y^2} = 4\) and the red area is the upper portion of \({x^2} + {z^2} = 4\) that is inside \({x^2} + {y^2} = 4\).
Now, in general, seeing this region would (and probably should) suggest that we use polar coordinates to do the integral. However, while using polar coordinates to do this integral wouldn’t be that difficult, (you might want to do it for the practice) it actually turns out to be easier (in this case!) to use Cartesian coordinates.
In terms of Cartesian coordinates let’s use the following limits for the red disk.
\[\begin{array}{c} - 2 \le x \le 2\\ - \sqrt {4 - {x^2}} \le y \le \sqrt {4 - {x^2}} \end{array}\]For the \(y\) limits we are just going from the lower portion of the circle to the upper portion of the circle.
Show Step 4Okay, let’s now set up the integral.
\[S = \iint\limits_{D}{{\frac{2}{{\sqrt {4 - {x^2}} }}\,dA}} = \int_{{ - 2}}^{2}{{\int_{{ - \sqrt {4 - {x^2}} }}^{{\sqrt {4 - {x^2}} }}{{\frac{2}{{\sqrt {4 - {x^2}} }}\,dy}}\,dx}}\] Show Step 5Next, let’s evaluate the integral.
\[\begin{align*}S & = \int_{{ - 2}}^{2}{{\int_{{ - \sqrt {4 - {x^2}} }}^{{\sqrt {4 - {x^2}} }}{{\frac{2}{{\sqrt {4 - {x^2}} }}\,dy}}\,dx}}\\ & = \int_{{ - 2}}^{2}{{\left. {\frac{2}{{\sqrt {4 - {x^2}} }}y} \right|_{ - \sqrt {4 - {x^2}} }^{\sqrt {4 - {x^2}} }\,dx}}\\ & = \int_{{ - 2}}^{2}{{\frac{2}{{\sqrt {4 - {x^2}} }}\left( {\sqrt {4 - {x^2}} - \left( { - \sqrt {4 - {x^2}} } \right)} \right)\,dx}}\\ & = \int_{{ - 2}}^{2}{{\frac{2}{{\sqrt {4 - {x^2}} }}\left( {2\sqrt {4 - {x^2}} } \right)\,dx}}\\ & \int_{{ - 2}}^{2}{{4\,dx}}\\ & = \left. {4x} \right|_{ - 2}^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{16}}\end{align*}\]We put in a few more steps that absolutely required here to make everything clear but you can see that keeping the integral in terms of Cartesian coordinates here was actually quite simple.
It just goes to show that there really are no hard and fast rules about doing things like converting to polar coordinates versus keeping things in Cartesian coordinates. While we are often taught to see a circle and just immediately convert to polar coordinates this problem has shown that there are the occasional problem that doesn’t require that to be done!
Show Step 6Okay, finally let’s get the surface area. So much of this problem was focused on what we did in the last couple of steps that it is easy to forget about just what we were doing.
Recall that the answer from Step 5 was just the surface area of the red portion of our surface. The full surface area is four times this and so the surface area of the whole surface is 16x4 = 64.