Section 17.3 : Surface Integrals
1. Evaluate \( \displaystyle \iint\limits_{S}{{z + 3y - {x^2}\,dS}}\) where \(S\) is the portion of \(z = 2 - 3y + {x^2}\) that lies over the triangle in the \(xy\)-plane with vertices \(\left( {0,0} \right)\), \(\left( {2,0} \right)\) and \(\left( {2, - 4} \right)\).
Show All Steps Hide All Steps
Start SolutionLet’s start off with a quick sketch of the surface we are working with in this problem.
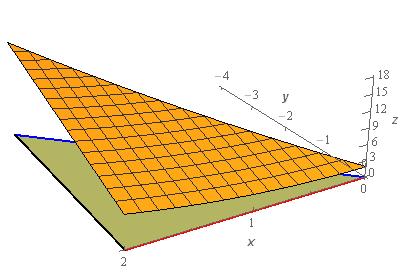
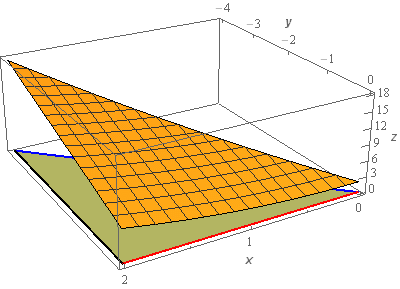
We included a sketch with traditional axes and a sketch with a set of “box” axes to help visualize the surface.
The orange surface is the sketch of \(z = 2 - 3y + {x^2}\) that we are working with in this problem. The greenish triangle below the surface is the triangle referenced in the problem statement that lies below the surface. This triangle will be the region \(D\) for this problem.
Here is a quick sketch of \(D\) just to get a better view of it than the mostly obscured view in the sketch above.
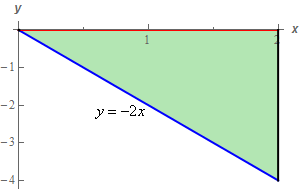
We could use either of the following sets of limits to describe \(D\).
We’ll decide which set to use in the integral once we get that set up.
Show Step 2Let’s get the integral set up now. In this case the surface is in the form,
\[z = g\left( {x,y} \right) = 2 - 3y + {x^2}\]so we’ll use the following formula for the surface integral.
\[\iint\limits_{S}{{f\left( {x,y,z} \right)\,dS}} = \iint\limits_{D}{{f\left( {x,y,g\left( {x,y} \right)} \right)\sqrt {{{\left( {\frac{{\partial g}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial g}}{{\partial y}}} \right)}^2} + 1} \,dA}}\]The integral is then,
\[\begin{align*}\iint\limits_{S}{{z + 3y - {x^2}\,dS}} & = \iint\limits_{D}{{\left[ {\left( {2 - 3y + {x^2}} \right) + 3y - {x^2}} \right]\sqrt {{{\left( {2x} \right)}^2} + {{\left( { - 3} \right)}^2} + 1} \,dA}}\\ & = \iint\limits_{D}{{2\sqrt {4{x^2} + 10} \,dA}}\end{align*}\]Don’t forget to plug the equation of the surface into \(z\) in the integrand and recall that \(D\) is the triangle sketched in Step 1.
Show Step 3Now all that we need to do is evaluate the double integral and that shouldn’t be too difficult at this point.
First note that from the integrand it should be pretty clear that we’ll want to integrate with respect to \(y\) first (unless you want to do a trig substitution of course….). So, the integral becomes,
\[\begin{align*}\iint\limits_{S}{{z + 3y - {x^2}\,dS}} & = \iint\limits_{D}{{2\sqrt {4{x^2} + 10} \,dA}}\\ & = \int_{0}^{2}{{\int_{{ - 2x}}^{0}{{2\sqrt {4{x^2} + 10} \,dy}}\,dx}}\\ & = \int_{0}^{2}{{\left. {\left( {2y\sqrt {4{x^2} + 10} } \right)} \right|_{ - 2x}^0\,dx}}\\ & = \int_{0}^{2}{{4x\sqrt {4{x^2} + 10} \,dx}}\\ & = \left. {\frac{1}{3}{{\left( {4{x^2} + 10} \right)}^{\frac{3}{2}}}} \right|_0^2 = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{1}{3}\left( {{{26}^{\frac{3}{2}}} - {{10}^{\frac{3}{2}}}} \right) = 33.6506}}\end{align*}\]