I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 5.6 : Definition of the Definite Integral
8. For \( \displaystyle \int_{1}^{4}{{3x - 2\,dx}}\) sketch the graph of the integrand and use the area interpretation of the definite integral to determine the value of the integral.
Show All Steps Hide All Steps
Start SolutionHere is the graph of the integrand, \(f\left( x \right) = 3x - 2\), on the interval \(\left[ {1,4} \right]\).
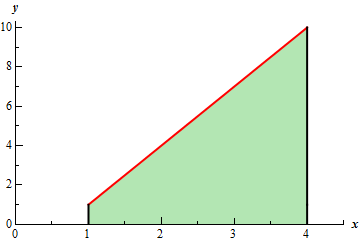
Now, we know that the integral is simply the area between the line and the \(x\)-axis and so we should be able to use basic area formulas to help us determine the value of the integral. Here is a “modified” graph that will help with this.
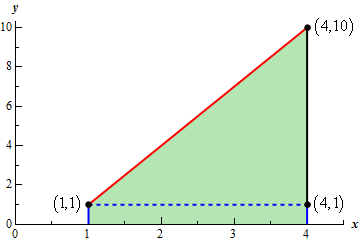
From this sketch we can see that we can think of this area as a rectangle with width 3 and height 1 and a triangle with base 3 and height 9. The value of the integral will then be the sum of the areas of the rectangle and the triangle.
Here is the value of the integral,
\[\int_{1}^{4}{{3x - 2\,dx}} = \left( 3 \right)\left( 1 \right) + \frac{1}{2}\left( 3 \right)\left( 9 \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{\frac{{33}}{2}}}\]