Section 5.6 : Definition of the Definite Integral
9. For \( \displaystyle \int_{0}^{5}{{ - 4x\,dx}}\) sketch the graph of the integrand and use the area interpretation of the definite integral to determine the value of the integral.
Show All Steps Hide All Steps
Start SolutionHere is the graph of the integrand, \(f\left( x \right) = - 4x\) on the interval \(\left[ {0,5} \right]\).
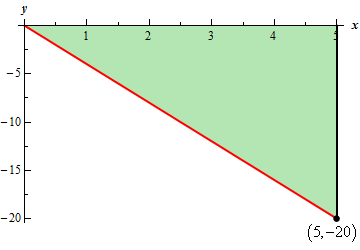
Now, we know that the integral is simply the area between the line and the \(x\)-axis and so we should be able to use basic area formulas to help us determine the value of the integral.
In this case we can see the area is clearly a triangle with base 5 and height 20. However, we need to be a little careful here and recall that area that is below the \(x\)-axis is considered to be negative area and so we’ll need to keep that in mind when we do the area computation.
Here is the value of the integral,
\[\int_{0}^{5}{{ - 4x\,dx}} = - \frac{1}{2}\left( 5 \right)\left( {20} \right) = \require{bbox} \bbox[2pt,border:1px solid black]{{ - 50}}\]