I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 3.2 : Interpretation of the Derivative
2. Use the graph of the function, \(f\left( x \right)\), estimate the value of \(f'\left( a \right)\) for
- \(a = 1\)
- \(a = 4\)
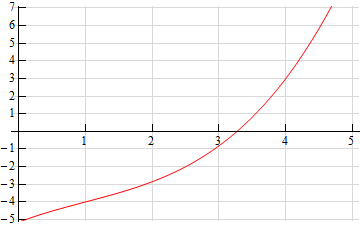
Show All Solutions Hide All Solutions
a \(a = 1\) Show All Steps Hide All StepsStart Solution
Given that one of the interpretations of the derivative is that it is the slope of the tangent line to the function at a particular point let’s first sketch in a tangent line at the point on the graph.
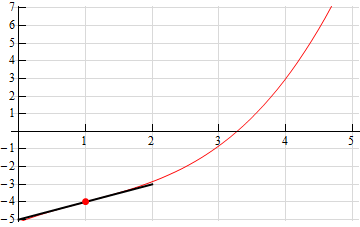
The function is clearly increasing here and so we know that the derivative at this point will be positive. Now, from this sketch of the tangent line it looks like if we run over 1 we go up 1 and so we can estimate that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{f'\left( 1 \right) = 1}}\]b \(a = 4\) Show All Steps Hide All Steps
Start Solution
Given that one of the interpretations of the derivative is that it is the slope of the tangent line to the function at a particular point. Let’s first sketch in a tangent line at the point.
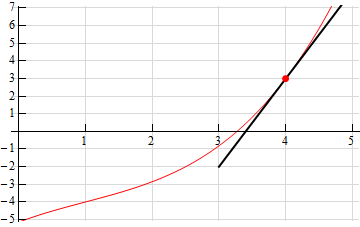
The function is clearly increasing here and so we know that the derivative at this point will be positive. Now, from this sketch of the tangent line it looks like if we run over 1 we go up 5 and so we can estimate that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{f'\left( 4 \right) = 5}}\]