Section 3.2 : Interpretation of the Derivative
3. Sketch the graph of a function that satisfies\(f\left( 1 \right) = 3\), \(f'\left( 1 \right) = 1\), \(f\left( 4 \right) = 5\), \(f'\left( 4 \right) = - 2\).
Show All Steps Hide All Steps
First, recall that one of the interpretations of the derivative is that it is the slope of the tangent line to the function at a particular point. So, let’s start off with a graph that has the given points on it and a sketch of a tangent line at the points whose slope is the value of the derivative at the points.
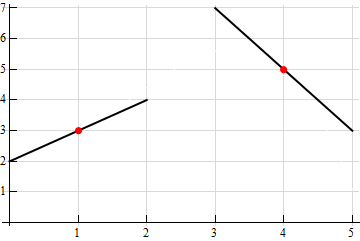
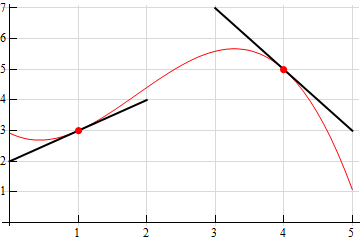
Now, all that we need to do is sketch in a graph that goes through the indicated points and at the same time it must be parallel to the tangents that we sketched. There are many possible sketches that we can make here and so don’t worry if your sketch is not the same as the one here. This is just one possible sketch that meets the given conditions.
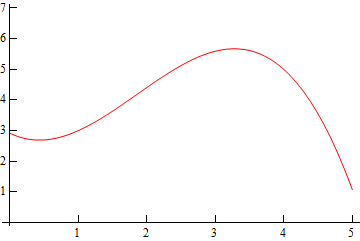
While, it’s not really needed here is a sketch of the function without all the extra bits that we put in to help with the sketch.