Section 3.2 : Interpretation of the Derivative
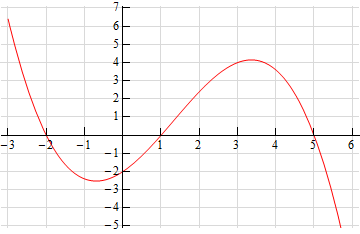
5. Below is the graph of some function, \(f\left( x \right)\). Use this to sketch the graph of the derivative, \(f'\left( x \right)\).
Show All Steps Hide All Steps
From the graph of the function it is pretty clear that we will have horizontal tangent lines at \(x = - 2\), \(x = 1\) and \(x = 5\). Because we will have horizontal tangents here we also know that the derivative at these points must be zero. Therefore, we know the following derivative evaluations.
\[f'\left( { - 2} \right) = 0\hspace{0.5in}f'\left( 1 \right) = 0\hspace{0.5in}f'\left( 5 \right) = 0\]The points we found above break the \(x\)-axis up into regions where the function is increasing and decreasing. Recall that if the derivative is positive then the function is increasing and likewise if the derivative is negative then the function is decreasing. Using these ideas we can easily identify the sign of the derivative on each of the regions. Doing this gives,
\[\begin{align*}\hspace{0.25in}x & < - 2 & \hspace{0.25in}f'\left( x \right) > 0\\ - 2 < x & < 1 & \hspace{0.25in}f'\left( x \right) < 0\\ 1 < x & < 5 & \hspace{0.25in}f'\left( x \right) > 0\\ x & > 5 & \hspace{0.25in}f'\left( x \right) < 0\end{align*}\]In the range \(x < - 2\) we know the derivative must be positive and that it must be zero at \(x = - 2\) so it makes sense that just to the left of \(x = - 2\) the derivative must be decreasing.
In the range \( - 2 < x < 1\)we know that the derivative will be negative and that it will be zero at the endpoints of the range. So, to the right of \(x = - 2\) the derivative will have to be decreasing (goes from zero to a negative number). Likewise, to the left of \(x = 1\) the derivative will have to be increasing (goes from a negative number to zero).
Note that we don’t really know just how the derivative will behave everywhere in this range, but we can use the general behavior near the endpoints and go with the simplest way to connect the two up to get an idea of what the derivative should look like.
Following similar reasoning we can see that the derivative should be increasing just to the right of \(x = 1\) (goes from zero to a positive number), decreasing just to the left of \(x = 5\) (goes from a positive number to zero) and decreasing just to the right of \(x = 5\) (goes from zero to a negative number).
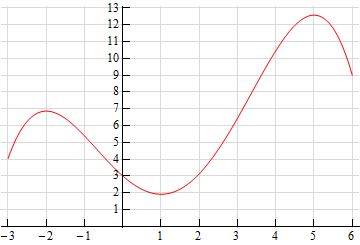
Show Step 4So, putting all of this together here is a sketch of the derivative. Note that we included the a scale on the vertical axis if you would like to try and estimate some specific values of the derivative as we did in Example 4 of this section.