Section 3.2 : Interpretation of the Derivative
6. Below is the graph of some function, \(f\left( x \right)\). Use this to sketch the graph of the derivative, \(f'\left( x \right)\).
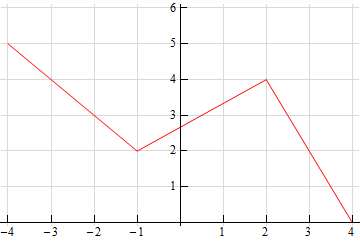
Show All Steps Hide All Steps
Because the three portions of the function are actually lines and the tangent line to a line would just be the line itself we can easily compute the derivative on each portion of the curve.
On each of the portions we can use the grid included on the graph to compute the slope of each part. Knowing the slope of the graph on each portion will in turn tell us the slope of the tangent line for each portion. This in turn tells us that the derivative on each of the three portions is then,
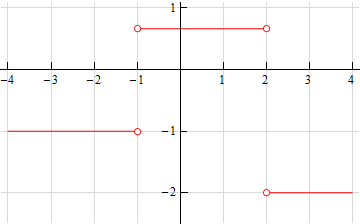
\[\begin{align*} x & < - 1 & \hspace{0.25in}f'\left( x \right) = - 1\\ - 1 < x & < 2 & \hspace{0.25in}f'\left( x \right) = \frac{2}{3}\\ x & > 2 & \hspace{0.25in}f'\left( x \right) = - 2\end{align*}\]Recall Example 4 from the previous section. In that example we showed that the derivative of the absolute value function does not exist at \(x = 0\). The limit on the left side of \(x = 0\) (which gives the slope of the line on the left) and the limit on the right side of \(x = 0\) (which gives the slope of the line on the right) were different and so the overall limit did not exist. This in turn tells us that the derivative doesn’t exist at that point.
Here we have the same problem. We’ll leave it to you to verify that the right and left-handed limits at \(x = - 1\) are not the same and so the derivative does not exist at \(x = - 1\). Likewise, the derivative does not exist at \(x = 2\).
There will therefore be open dots on the graph at these two points.
Show Step 3Here is the sketch of the derivative of this function.