Section 2.6 : Infinite Limits
2. For \(\displaystyle h\left( t \right) = \frac{{2t}}{{6 + t}}\) evaluate,
- \(\mathop {\lim }\limits_{t \to \, - {6^{\, - }}} h\left( t \right)\)
- \(\mathop {\lim }\limits_{t \to \, - {6^{\, + }}} h\left( t \right)\)
- \(\mathop {\lim }\limits_{t \to \, - 6} h\left( t \right)\)
Show All Solutions Hide All Solutions
a \(\mathop {\lim }\limits_{t \to \, - {6^{\, - }}} h\left( t \right)\) Show SolutionLet’s start off by acknowledging that for \(t \to - {6^ - }\) we know \(t < - 6\).
For the numerator we can see that, in the limit, we will get -12.
The denominator takes a little more work. Clearly, in the limit, we have,
\[6 + t \to 0\]but we can actually go a little farther. Because we know that \(t < - 6\) we also know that,
\[6 + t < 0\]More compactly, we can say that in the limit we will have,
\[6 + t \to {0^ - }\]So, in the limit, the numerator is approaching a negative number and the denominator is an increasingly small negative number. The quotient must then be an increasing large positive number or,
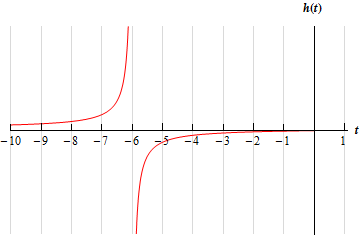
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{t \to \, - {6^{\, - }}} \frac{{2t}}{{6 + t}} = \infty }}\]Note that this also means that there is a vertical asymptote at \(t = - 6\).
b \(\mathop {\lim }\limits_{t \to \, - {6^{\, + }}} h\left( t \right)\) Show Solution
Let’s start off by acknowledging that for \(t \to - {6^ + }\) we know \(t > - 6\).
For the numerator we can see that, in the limit, we will get -12.
The denominator will also work similarly to the first part. In the limit, we have,
\[6 + t \to 0\]but we can actually go a little farther. Because we know that \(t > - 6\) we also know that,
\[6 + t > 0\]More compactly, we can say that in the limit we will have,
\[6 + t \to {0^ + }\]So, in the limit, the numerator is approaching a negative number and the denominator is an increasingly small positive number. The quotient must then be an increasing large negative number or,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{t \to \, - {6^{\, + }}} \frac{{2t}}{{6 + t}} = - \infty }}\]Note that this also means that there is a vertical asymptote at \(t = - 6\), which we already knew from the first part.
c \(\mathop {\lim }\limits_{t \to \, - 6} h\left( t \right)\) Show Solution
In this case we can see from the first two parts that,
\[\mathop {\lim }\limits_{t \to \, - {6^{\, - }}} h\left( t \right) \ne \mathop {\lim }\limits_{t \to \, - {6^{\, + }}} h\left( t \right)\]and so, from our basic limit properties we can see that \(\mathop {\lim }\limits_{t \to \, - 6} h\left( t \right)\) does not exist.
For the sake of completeness and to verify the answers for this problem here is a quick sketch of the function.