I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 2.6 : Infinite Limits
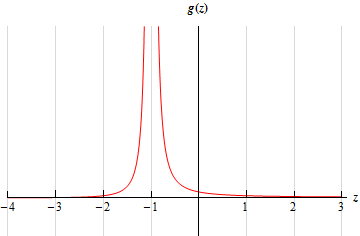
3. For \(\displaystyle g\left( z \right) = \frac{{z + 3}}{{{{\left( {z + 1} \right)}^2}}}\) evaluate,
- \(\mathop {\lim }\limits_{z \to \, - {1^{\, - }}} g\left( z \right)\)
- \(\mathop {\lim }\limits_{z \to \, - {1^{\, + }}} g\left( z \right)\)
- \(\mathop {\lim }\limits_{z \to \, - 1} g\left( z \right)\)
Show All Solutions Hide All Solutions
a \(\mathop {\lim }\limits_{z \to \, - {1^{\, - }}} g\left( z \right)\) Show SolutionLet’s start off by acknowledging that for \(z \to - {1^ - }\) we know \(z < - 1\).
For the numerator we can see that, in the limit, we will get 2.
Now let’s take care of the denominator. In the limit, we will have,
\[z + 1 \to {0^ - }\]and upon squaring the \(z + 1\) we see that, in the limit, we will have,
\[{\left( {z + 1} \right)^2} \to {0^ + }\]So, in the limit, the numerator is approaching a positive number and the denominator is an increasingly small positive number. The quotient must then be an increasing large positive number or,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{z \to \, - {1^{\, - }}} \frac{{z + 3}}{{{{\left( {z + 1} \right)}^2}}} = \infty }}\]Note that this also means that there is a vertical asymptote at \(z = - 1\).
b \(\mathop {\lim }\limits_{z \to \, - {1^{\, + }}} g\left( z \right)\) Show Solution
Let’s start off by acknowledging that for \(z \to - {1^ + }\) we know \(z > - 1\).
For the numerator we can see that, in the limit, we will get 2.
Now let’s take care of the denominator. In the limit, we will have,
\[z + 1 \to {0^ + }\]and upon squaring the \(z + 1\) we see that, in the limit, we will have,
\[{\left( {z + 1} \right)^2} \to {0^ + }\]So, in the limit, the numerator is approaching a positive number and the denominator is an increasingly small positive number. The quotient must then be an increasing large positive number or,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{z \to \, - {1^{\, + }}} \frac{{z + 3}}{{{{\left( {z + 1} \right)}^2}}} = \infty }}\]Note that this also means that there is a vertical asymptote at \(z = - 1\), which we already knew from the first part.
c \(\mathop {\lim }\limits_{z \to \, - 1} g\left( z \right)\) Show Solution
In this case we can see from the first two parts that,
\[\mathop {\lim }\limits_{z \to \, - {1^{\, - }}} g\left( z \right) = \mathop {\lim }\limits_{z \to \, - {1^{\, + }}} g\left( z \right) = \infty \]and so, from our basic limit properties we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{z \to \, - 1} g\left( z \right) = \infty }}\]For the sake of completeness and to verify the answers for this problem here is a quick sketch of the function.