Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 2.6 : Infinite Limits
6. For \(\displaystyle R\left( y \right) = \tan \left( y \right)\) evaluate,
- \(\mathop {\lim }\limits_{y \to {{{\textstyle{{3\pi } \over 2}}}^{\, - }}} R\left( y \right)\)
- \(\mathop {\lim }\limits_{y \to {{{\textstyle{{3\pi } \over 2}}}^{\, + }}} R\left( y \right)\)
- \(\mathop {\lim }\limits_{y \to {\textstyle{{3\pi } \over 2}}} R\left( y \right)\)
Hint : Don’t forget the graph of the tangent function.
Show All Solutions Hide All Solutions
a Show SolutionThe easiest way to do this problem is from the graph of the tangent function so here is a quick sketch of the tangent function over several periods.
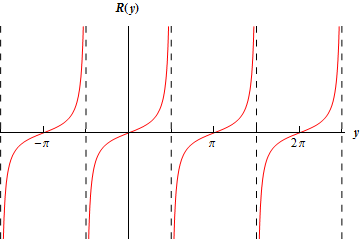
From the sketch we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{y \to {{{\textstyle{{3\pi } \over 2}}}^{\, - }}} \tan \left( y \right) = \infty }}\]b Show Solution
From the graph in the first part we can see that,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\mathop {\lim }\limits_{y \to {{{\textstyle{{3\pi } \over 2}}}^{\, + }}} \tan \left( y \right) = - \infty }}\]c Show Solution
From the first two parts that,
\[\mathop {\lim }\limits_{y \to {{{\textstyle{{3\pi } \over 2}}}^{\, - }}} R\left( y \right) \ne \mathop {\lim }\limits_{y \to {{{\textstyle{{3\pi } \over 2}}}^{\, + }}} R\left( y \right)\]and so, from our basic limit properties we can see that \(\mathop {\lim }\limits_{y \to {\textstyle{{3\pi } \over 2}}} R\left( y \right)\) does not exist.