Okay, let’s start off by acknowledging that for \(x \to {0^ - }\) we know \(x < 0\) and so \( - x > 0\) or,

What this means for us is that this limit does make sense! We know that we can’t have negative arguments in a logarithm, but because of the negative sign in this particular logarithm that means that we can use negative \(x\)’s in this function (positive \(x\)’s on the other hand will now cause problems of course…).

By Example 6 in the notes for this section we know that as the argument of a logarithm approaches zero from the right (as ours does in this limit) then the logarithm will approach \( - \infty \).

Therefore, the answer for this part is,

In this part we know that for \(x \to {0^ + }\) we have \(x > 0\) and so \( - x < 0\). At this point we can stop. We know that we can’t have negative arguments in a logarithm and for this limit that is exactly what we’ll get and so \(\mathop {\lim }\limits_{x \to {0^{\, + }}} h\left( x \right)\) does not exist.

The answer for this part is \(\mathop {\lim }\limits_{x \to 0} h\left( x \right)\) does not exist. We can use two lines of reasoning to justify this.

First, we are unable to look at both sides of the point in question and so there is no possible way for the limit to exist.

The second line of reasoning is really the same as the first but put in different terms. From the first two parts that,

and so, from our basic limit properties we can see that \(\mathop {\lim }\limits_{x \to 0} h\left( x \right)\) does not exist.

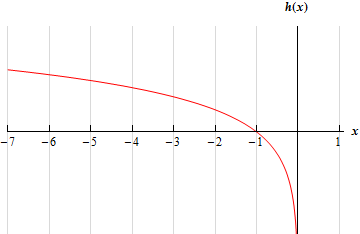
For the sake of completeness and to verify the answers for this problem here is a quick sketch of the function.