Section 4.9 : More Optimization
1. We want to construct a window whose middle is a rectangle and the top and bottom of the window are semi-circles. If we have 50 meters of framing material what are the dimensions of the window that will let in the most light?
Show All Steps Hide All Steps
Start SolutionLet’s start with a quick sketch of the window.
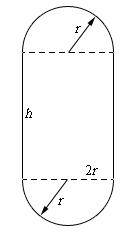
Next, we need to set up the constraint and equation that we are being asked to optimize.
We are told that we have 50 meters of framing material (i.e. the perimeter of the window) and so that will be the constraint for this problem.
\[50 = 2h + 2\left( {\pi r} \right) = 2h + 2\pi r\]We are being asked to maximize the amount of light being let in and that is simply the enclosed area or,
\[A = h\left( {2r} \right) + 2\left( {{\frac{1}{2}}\pi {r^2}} \right) = 2hr + \pi {r^2}\]With both of these equations we were a little careful with the last term. In each case we needed either the perimeter or area of each semicircle and there were two of them. The end result of course is the equation of the perimeter/area of a whole circle, but we really should be careful setting these equations up and note just where everything is coming from.
Show Step 3Now, let’s solve the constraint for \(h\).
\[h = 25 - \pi r\]Plugging this into the area function gives,
\[A\left( r \right) = 2\left( {25 - \pi r} \right)r + \pi {r^2} = 50r - \pi {r^2}\] Show Step 4Finding the critical point(s) for this shouldn’t be too difficult at this point. Here is the derivative.
\[A'\left( r \right) = 50 - 2\pi r\]From this it looks like we get a single critical points : \(r = \frac{25}{\pi} = 7.9577\).
Show Step 5The second derivative of the volume function is,
\[A''\left( r \right) = - 2\pi \]From this we can see that the second derivative is always negative. Therefore \(A\left( r \right)\) will always be concave down and so the single critical point we got in Step 4 must be a relative maximum and hence must be the value that allows in the maximum amount of light.
Show Step 6Now, let’s finish the problem by getting the radius of the semicircles.
\[h = 25 - \pi \left( \frac{25}{\pi} \right) = 0\]Okay, what this means is that in fact the most light will come from not even having a rectangle between the semicircles and just having a circular window of radius \(r = \frac{25}{\pi}\).