Section 4.9 : More Optimization
2. Determine the area of the largest rectangle that can be inscribed in a circle of radius 1.
Show All Steps Hide All Steps
Start SolutionLet’s start with a quick sketch of the circle and rectangle. Also, in order to make the work a little easier we went ahead and assumed that the circle was centered at the origin of the standard \(xy\)-coordinate system.
We’ve also defined a point \(\left( {x,y} \right)\) in the first quadrant. This is the point that we will be attempting to find when we get into the problems. If we know the coordinates of this point then the rectangle defined by the point, as shown in the figure, will be the one with the largest area.
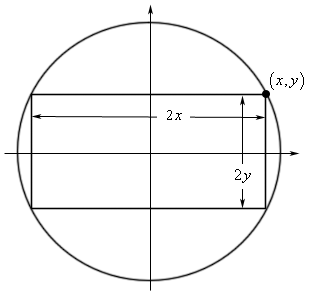
Next, we need to set up the constraint and equation that we are being asked to optimize.
Given our graph above we can easily determine the equation of the circle. This will also be the constraint of the problem because the corners of the rectangle must be on the circle.
\[{x^2} + {y^2} = 1\]Also note that from the figure or equation we can clearly see that \( - 1 \le x \le 1\) and \( - 1 \le y \le 1\). One or both of these limits will be useful later on in the problem.
We are being asked to maximize the amount of the rectangle and using the definitions we see in the figure above the area is,
\[A = \left( {2x} \right)\left( {2y} \right) = 4xy\] Show Step 3We can solve the constraint for \(x\) or \(y\). Either will lead to essentially the same work so we’ll solve for \(x\).
\[x = \pm \sqrt {1 - {y^2}} \]Because we’ve defined the point on the circle to be in the 1st quadrant we will use the “+” portion of this. Plugging this into the area function gives,
\[A\left( y \right) = 4y\sqrt {1 - {y^2}} \] Show Step 4Finding the critical point(s) for this shouldn’t be too difficult at this point. Here is the derivative.
\[A'\left( y \right) = 4\sqrt {1 - {y^2}} - \frac{{4{y^2}}}{{\sqrt {1 - {y^2}} }} = \frac{{4 - 8{y^2}}}{{\sqrt {1 - {y^2}} }}\]From this it looks like, from the numerator, we get the critical points,
\[y = \pm \sqrt {{\frac{1}{2}}} = \pm \frac{1}{\sqrt{2}} = \pm 0.7071\]From the denominator we get the critical points : \(y = \pm 1\) and yes these are critical points because the function will exist at these points.
Before proceeding to the next step let’s notice that because our point is in the first quadrant we know that \(y\) must be positive. This fact along with the limits on \(y\) we discussed in Step 2 tells us that we must have : \(0 \le y \le 1\).
This in turn tells us that the only two critical points that we need to worry about are,
\[y = \frac{1}{\sqrt{2}} = 0.7071\hspace{0.5in}y = 1\] Show Step 5Because we’ve got a range for possible critical points all we need to do to determine the maximum area is plug the end points and critical points into the area.
\[A\left( 0 \right) = 0\hspace{0.5in}A\left( \frac{1}{\sqrt{2}} \right) = 2\hspace{0.5in}A\left( 1 \right) = 0\] Show Step 6So, the area of the largest rectangle that can be inscribed in the circle is : 2.