Section 4.9 : More Optimization
3. Find the point(s) on \(x = 3 - 2{y^2}\) that are closest to \(\left( { - 4,0} \right)\).
Show All Steps Hide All Steps
Start SolutionLet’s start with a quick sketch of this situation. Below is a sketch of the graph of the function as well as the point \(\left( { - 4,0} \right)\). As we can see we can expect to get two points as answers with the only difference being the sign on the \(y\)-coordinate.
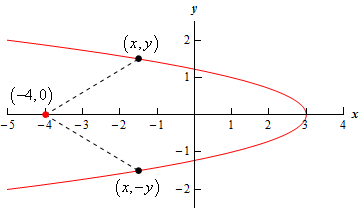
Next, we need to set up the constraint and equation that we are being asked to optimize.
In this case the constraint is simply the equation we are given. The point must lie on the graph and so must also satisfy the equation.
\[x = 3 - 2{y^2}\]We are being asked to minimize the distance between a point (or points) on the graph and the point \(\left( { - 4,0} \right)\). We can do this by looking at the distance between \(\left( { - 4,0} \right)\) and \(\left( {x,y} \right)\). The distance between these two points is,
\[d = \sqrt {{{\left( {x + 4} \right)}^2} + {y^2}} \]As we discussed in the notes for this section the point that minimizes the square of the distance will also minimize the distance itself and so to avoid dealing with the root we will minimize the square of the distance or,
\[{d^2} = {\left( {x + 4} \right)^2} + {y^2}\] Show Step 3Now we have two choices on how to proceed from this point. The first option is to plug the equation we are given into the \(x\) in the distance squared and get a 4th degree polynomial for \(y\) that we’ll need to work with. The second is to solve the equation for \({y^2}\) and plug that into the distance squared and get a 2nd degree polynomial for \(x\) that we’ll need to work with. The second option gives a “nicer” polynomial to work with so we’ll do that.
\[{y^2} = {\frac{1}{2}}\left( {3 - x} \right) = {\frac{3}{2}} - {\frac{1}{2}}x\]Plugging this into the distance squared gives,
\[f\left( x \right) = {d^2} = {\left( {x + 4} \right)^2} + {\frac{3}{2}} - {\frac{1}{2}}x = {x^2} + {\frac{15}{2}}x + {\frac{35}{2}}\] Show Step 4Finding the critical point(s) for this shouldn’t be too difficult at this point. Here is the derivative.
\[f'\left( x \right) = 2x + {\frac{15}{2}}\]From this it looks like we get a single critical point : \(x = - {\frac{15}{4}} = - 3.75\).
Show Step 5The second derivative of the distance squared function is,
\[f''\left( x \right) = 2\]From this we can see that the second derivative is always positive. Therefore, the distance squared will always be concave up and so the single critical point we got in Step 4 must be a relative minimum and hence must be the value of \(x\) that gives the points that are closest to \(\left( { - 4,0} \right)\).
Show Step 6Finally, we just need to determine the values \(y\) that give the actual points.
\[{y^2} = {\frac{3}{2}} - {\frac{1}{2}}\left( { - {\frac{15}{4}}} \right) = {\frac{27}{8}}\hspace{0.5in} \Rightarrow \hspace{0.5in}y = \pm \sqrt {{\frac{27}{8}}} = \pm 1.8371\]So, the two points on the graph that are closest to \(\left( { - 4,0} \right)\) are,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{\left( { - {\frac{15}{4}},\sqrt {{\frac{27}{8}}} } \right)\hspace{0.5in} \& \hspace{0.5in}\left( { - {\frac{15}{4}}, - \sqrt {{\frac{27}{8}}} } \right)}}\]