Section 4.8 : Optimization
6. We want to build a box whose base length is 6 times the base width and the box will enclose 20 in3. The cost of the material of the sides is $3/in2 and the cost of the top and bottom is $15/in2. Determine the dimensions of the box that will minimize the cost.
Show All Steps Hide All Steps
Start SolutionThe first step is to do a quick sketch of the problem. We could probably skip the sketch in this case, but that is a really bad habit to get into. For many of these problems a sketch is really convenient and it can be used to help us keep track of some of the important information in the problem and to “define” variables for the problem.
Here is the sketch for this problem.
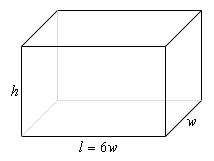
Next, we need to set up the constraint and equation that we are being asked to optimize.
We are told that the volume of the box must be 20 in3 and so this is the constraint.
\[20 = lwh = 6{w^2}h\] We are being asked to minimize the cost and the cost function is, \[C = 3\left[ {2\left( {lh} \right) + 2\left( {wh} \right)} \right] + 15\left[ {2\left( {lw} \right)} \right] = 3\left[ {12wh + 2wh} \right] + 15\left[ {12{w^2}} \right] = 42wh + 180{w^2}\]Note as well that we went ahead and used fact that \(l = 6w\) in both of these equations to reduce the three variables in the equation down to two variables.
Show Step 3Now, let’s solve the constraint for \(h\) (that will allow us to avoid dealing with roots).
\[h = \frac{{10}}{{3{w^2}}}\]Plugging this into the cost function gives,
\[C\left( w \right) = 42w\left( {\frac{{10}}{{3{w^2}}}} \right) + 180{w^2} = \frac{{140}}{w} + 180{w^2}\] Show Step 4Finding the critical point(s) for this shouldn’t be too difficult at this point. Here is the derivative.
\[C'\left( w \right) = - \frac{140}{w^2} + 360w = \frac{{360{w^3} - 140}}{{{w^2}}}\]From this it looks like the only critical point is : \(w = \sqrt[3]{\frac{7}{18}} = 0.7299\).
Note that \(w=0\) can’t be a critical point because the function does not exist there.
Show Step 5The second derivative of the volume function is,
\[C''\left( w \right) = \frac{{280}}{{{w^3}}} + 360\]From this we can see that the second derivative is always positive for positive \(w\) (which we will always have for this case since \(w\) is the width of a box). Therefore, provided \(w\) is positive, \(C\left( w \right)\) will always be concave up and so the single critical point we got in Step 4 must be a relative minimum and hence must be the value that gives a minimum cost.
Show Step 6Now, let’s finish the problem by getting the remaining dimensions.
\[l = 6w = 4.3794\hspace{0.5in}h = \frac{{10}}{{3{{\left( {0.7299} \right)}^2}}} = 6.2568\]The final dimensions are then,
\[\require{bbox} \bbox[2pt,border:1px solid black]{{w = 0.7299\hspace{0.5in}\,l = 4.3794\hspace{0.5in}\,\,h = 6.2568}}\]