Section 4.8 : Optimization
8. We have a piece of cardboard that is 50 cm by 20 cm and we are going to cut out the corners and fold up the sides to form a box. Determine the height of the box that will give a maximum volume.

Show All Steps Hide All Steps
Start SolutionThe first step is to do a quick sketch of the problem.
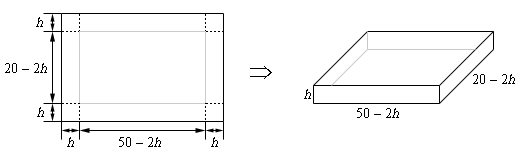
As with the problem like this in the notes the constraint is really the size of the box and that has been taken into account in the figure so all we need to do is set up the volume equation that we want to maximize.
\[V\left( h \right) = h\left( {50 - 2h} \right)\left( {20 - 2h} \right) = 4{h^3} - 140{h^2} + 1000h\] Show Step 3Finding the critical point(s) for this shouldn’t be too difficult at this point so here is that work,
\[V'\left( h \right) = 12{h^2} - 280h + 1000\hspace{0.75in}h = \frac{35 \pm 5\sqrt {19}}{3} = 4.4018,\,\,18.9315\]From the figure above, we can see that the limits on \(h\) must be \(h = 0\) and \(h = 10\) (the largest \(h\) could be is ½ the smaller side). Note that neither of these really make physical sense but they do provide limits on \(h\).
So, we must have \(0 \le h \le 10\) and this eliminates the second critical point and so the only critical point we need to worry about is \(h = 4.4018\)
Show Step 4Because we have limits on \(h\) we can quickly check to see if we have maximum by plugging in the volume function.
\[V\left( 0 \right) = 0\hspace{0.75in}V\left( {4.4018} \right) = 2030.34\hspace{0.75in}V\left( {10} \right) = 0\]So, we can see then that the height of the box will have to be \(\require{bbox} \bbox[2pt,border:1px solid black]{{h = 4.4018}}\) in order to get a maximum volume.