Section 3.11 : Related Rates
10. A tank of water in the shape of a cone is being filled with water at a rate of 12 m3/sec. The base radius of the tank is 26 meters and the height of the tank is 8 meters. At what rate is the depth of the water in the tank changing when the radius of the top of the water is 10 meters?

Show All Steps Hide All Steps
Start SolutionHere is a sketch of the cross section of the tank and it is not even remotely to scale as I found it easier to reuse an old image that I had lying around. I can be a little lazy sometimes. At least I was less lazy with the image in the problem statement….
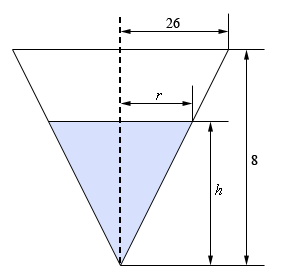
We want to determine \(h'\) when \(r = 10\) and we know that \(V' = 12\).
Show Step 2We’ll need the equation for the volume of a cone.
\[V = {\textstyle{1 \over 3}}\pi {r^2}h\]This is a problem however as it has both \(r\) and \(h\) in it and it would be best to have only \(h\) since we need \(h'\). We can use similar triangles to fix this up. Based on similar triangles we get the following equation which can be solved for \(r\).
\[\frac{r}{h} = \frac{{26}}{8}\hspace{0.5in} \Rightarrow \hspace{0.5in}r = {\textstyle{{13} \over 4}}h\]Plugging this into the volume equation gives,
\[V = {\textstyle{{169} \over {48}}}\pi {h^3}\] Show Step 3Next, let’s differentiate this with respect to \(t\).
\[V' = {\textstyle{{169} \over {16}}}\pi {h^2}h'\] Show Step 4To finish off this problem all we need to do is determine the value of \(h\) for the time we are interested in. This can easily be done from the similar triangle equation and the fact that we know \(r = 10\).
\[h = {\textstyle{4 \over {13}}}r = {\textstyle{4 \over {13}}}\left( {10} \right) = {\textstyle{{40} \over {13}}}\]The rate of change of the height of the water is then,
\[12 = {\textstyle{{169} \over {16}}}\pi {\left( {{\textstyle{{40} \over {13}}}} \right)^2}h' = 100\pi h'\hspace{0.5in} \Rightarrow \hspace{0.5in}\require{bbox} \bbox[2pt,border:1px solid black]{{h' = {\textstyle{3 \over {25\pi }}}}}\]