Mobile Notice
You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone). Due to the nature of the mathematics on this site it is best viewed in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (you should be able to scroll/swipe to see them) and some of the menu items will be cut off due to the narrow screen width.
Section 3.11 : Related Rates
- In the following assume that \(x\) and \(y\) are both functions of \(t\). Given \(x = - 2\), \(y = 1\) and \(x' = - 4\) determine \(y'\) for the following equation. \[6{y^2} + {x^2} = 2 - {x^3}{{\bf{e}}^{4 - 4y}}\] Solution
- In the following assume that \(x\), \(y\) and \(z\) are all functions of \(t\). Given \(x = 4\), \(y = - 2\), \(z = 1\), \(x' = 9\) and \(y' = - 3\) determine \(z'\) for the following equation. \[x\left( {1 - y} \right) + 5{z^3} = {y^2}{z^2} + {x^2} - 3\] Solution
- For a certain rectangle the length of one side is always three times the length of the other side.
- If the shorter side is decreasing at a rate of 2 inches/minute at what rate is the longer side decreasing?
- At what rate is the enclosed area decreasing when the shorter side is 6 inches long and is decreasing at a rate of 2 inches/minute?
- A thin sheet of ice is in the form of a circle. If the ice is melting in such a way that the area of the sheet is decreasing at a rate of 0.5 m2/sec at what rate is the radius decreasing when the area of the sheet is 12 m2? Solution
- A person is standing 350 feet away from a model rocket that is fired straight up into the air at a rate of 15 ft/sec. At what rate is the distance between the person and the rocket increasing (a) 20 seconds after liftoff? (b) 1 minute after liftoff? Solution
- A plane is 750 meters in the air flying parallel to the ground at a speed of 100 m/s and is initially 2.5 kilometers away from a radar station. At what rate is the distance between the plane and the radar station changing (a) initially and (b) 30 seconds after it passes over the radar station?
Solution

- Two people are at an elevator. At the same time one person starts to walk away from the elevator at a rate of 2 ft/sec and the other person starts going up in the elevator at a rate of 7 ft/sec. What rate is the distance between the two people changing 15 seconds later?
Solution

- Two people on bikes are at the same place. One of the bikers starts riding directly north at a rate of 8 m/sec. Five seconds after the first biker started riding north the second starts to ride directly east at a rate of 5 m/sec. At what rate is the distance between the two riders increasing 20 seconds after the second person started riding?
Solution

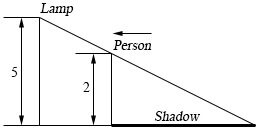
- A light is mounted on a wall 5 meters above the ground. A 2 meter tall person is initially 10 meters from the wall and is moving towards the wall at a rate of 0.5 m/sec. After 4 seconds of moving is the tip of the shadow moving (a) towards or away from the person and (b) towards or away from the wall?
Solution
- A tank of water in the shape of a cone is being filled with water at a rate of 12 m3/sec. The base radius of the tank is 26 meters and the height of the tank is 8 meters. At what rate is the depth of the water in the tank changing when the radius of the top of the water is 10 meters? Note the image below is not completely to scale….
Solution

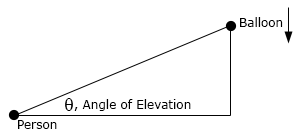
- The angle of elevation is the angle formed by a horizontal line and a line joining the observer’s eye to an object above the horizontal line. A person is 500 feet way from the launch point of a hot air balloon. The hot air balloon is starting to come back down at a rate of 15 ft/sec. At what rate is the angle of elevation, \(\theta \), changing when the hot air balloon is 200 feet above the ground. See the (probably bad) sketch below to help visualize the angle of elevation if you are having trouble seeing it.
Solution