I have been informed that on March 7th from 6:00am to 6:00pm Central Time Lamar University will be doing some maintenance to replace a faulty UPS component and to do this they will be completely powering down their data center.
Unfortunately, this means that the site will be down during this time. I apologize for any inconvenience this might cause.
Paul
February 18, 2026
Section 3.11 : Related Rates
7. Two people are at an elevator. At the same time one person starts to walk away from the elevator at a rate of 2 ft/sec and the other person starts going up in the elevator at a rate of 7 ft/sec. What rate is the distance between the two people changing 15 seconds later?
Show All Steps Hide All Steps
Start SolutionHere is a sketch for this part.
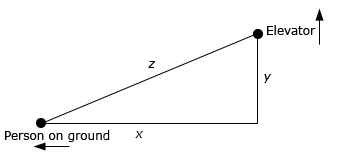
We want to determine \(z'\) after 15 seconds given that \(x' = 2\), \(y' = 7\) and assuming that they start at the same point.
Show Step 2Hopefully it’s clear that we’ll need the Pythagorean Theorem to solve this problem so here is that.
\[{z^2} = {x^2} + {y^2}\] Show Step 3Finally, let’s differentiate this with respect to \(t\) and we can even solve it for \(z'\) so the actual solution will be quick and simple to find.
\[2z\,z' = 2x\,x' + 2y\,y'\hspace{0.5in} \Rightarrow \hspace{0.5in}z' = \frac{{x\,x' + y\,y'}}{z}\] Show Step 4To finish off this problem all we need to do is determine all three lengths of the triangle in the sketch above. We can find \(x\) and \(y\) using their speeds and time while we can find \(z\) by reusing the Pythagorean Theorem.
\[\begin{array}{c}x = \left( 2 \right)\left( {15} \right) = 30\hspace{1.0in}y = \left( 7 \right)\left( {15} \right) = 105\\ z = \sqrt {{{30}^2} + {{105}^2}} = \sqrt {11925} = 15\sqrt {53} = 109.2016\end{array}\]The rate of change of the distance between the two people is then,
\[z' = \frac{{\left( {30} \right)\left( 2 \right) + \left( {105} \right)\left( 7 \right)}}{{109.2016}} = \require{bbox} \bbox[2pt,border:1px solid black]{{7.2801}}\]